河南省许昌市建安区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2021-05-08 类型:期中考试
一、单选题
-
1. 若式子 在实数范围内有意义,则a的取值范围是( )A、 B、 C、 D、2. 下列各组线段a、b、c能构成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 下列各式属于最简二次根式的是( )A、 B、 C、 D、4. 下列计算错误的是( )A、 B、 C、 D、5. 下列命题中错误的是( )A、直角三角形斜边上的中线等于斜边的一半 B、对角线互相垂直的四边形是菱形 C、三个角是直角的四边形是矩形 D、对角线互相垂直且相等的平行四边形是正方形6. 如图,四边形 中, , , ,如果 则 等于( )
 A、 B、 C、 D、7. 如图,点P是平面坐标系中一点,则点P到原点的距离是( )
A、 B、 C、 D、7. 如图,点P是平面坐标系中一点,则点P到原点的距离是( )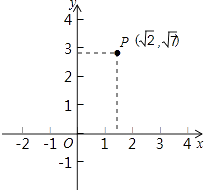 A、3 B、 C、 D、8. 已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )
A、3 B、 C、 D、8. 已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )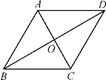 A、16 B、16 C、8 D、89. 如图,点O是矩形 的对角线 的中点, 交 于点M,若 , ,则 的长为( )
A、16 B、16 C、8 D、89. 如图,点O是矩形 的对角线 的中点, 交 于点M,若 , ,则 的长为( ) A、5 B、4 C、 D、10. 如图,在长方形 中无重叠放入面积分别为 和 的两张正方形纸片,则图中空白部分的面积为( )
A、5 B、4 C、 D、10. 如图,在长方形 中无重叠放入面积分别为 和 的两张正方形纸片,则图中空白部分的面积为( )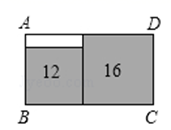 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知a<2,则 =.12. 已知 ,则x+y= .13. 请写出数学命题“勾股定理”的含义,如果 , 那么.14. 在四边形ABCD中,对角线AC , BD交于点O且AC , BD互相平分,若添加一个条件使得四边形ABCD是矩形,则这个条件可以是(填写一个即可).
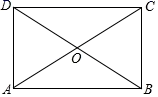 15. 如图,矩形纸片 中, , ,折叠纸片使 边与对角线 重合,折痕为 ,则折痕处G点与A点的距离为.
15. 如图,矩形纸片 中, , ,折叠纸片使 边与对角线 重合,折痕为 ,则折痕处G点与A点的距离为.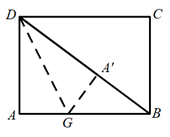
三、解答题
-
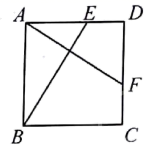
16. 计算:(1)、(2)、17. 如图所示, 是一个正方形花园,E,F是它的两个门,且 .要修建两条路 和 ,这两条路等长吗?它们有什么位置关系?为什么?
 18. 如图,E是 的边 的中点,连接 并延长交 的延长线于F,若 ,求 的长.
18. 如图,E是 的边 的中点,连接 并延长交 的延长线于F,若 ,求 的长. 19. 如图,每个小正方形的边长为1.
19. 如图,每个小正方形的边长为1. (1)、求出四边形 的周长;(2)、求证: .20. 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)、求出四边形 的周长;(2)、求证: .20. 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.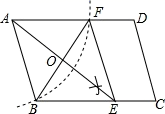 (1)、求证:四边形ABEF为菱形;(2)、AE,BF相交于点O,若BF=6,AB=5,求AE的长.21. 在化简 时,为了使式子的分母中不含根号,需要对原式进行恒等变形,这种变形我们称为分母有理化.甲、乙两位同学的做法如下:
(1)、求证:四边形ABEF为菱形;(2)、AE,BF相交于点O,若BF=6,AB=5,求AE的长.21. 在化简 时,为了使式子的分母中不含根号,需要对原式进行恒等变形,这种变形我们称为分母有理化.甲、乙两位同学的做法如下:甲:
乙:
(1)、你认为甲乙两人的做法( )A、甲乙两人都对 B、甲错乙对 C、甲对乙错 D、甲乙两人都错(2)、根据你对甲、乙同学解题方法的理解,请你使用一种方法对下面式子进行分母有理化.化简: