河南省信阳市潢川县2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2021-05-08 类型:期中考试
一、单选题
-
1. 函数y= 中自变量x的取值范围是( )A、x>2 B、x≥2 C、x≤2 D、x≠22. 下列各式属于最简二次根式的是( )
A、 B、 C、 D、3. 下列计算,正确的是( )A、 B、 C、 D、4. 为三个整数,若 , , ,则下列有关于 的大小关系,正确的是( ).A、 B、 C、 D、5. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )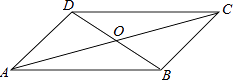 A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC6. 如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC6. 如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( ) A、3和2 B、2和3 C、4和1 D、1和47. 顺次连接对角线相等的四边形的各边中点,所形成的四边形是( )A、平行四边形 B、菱形 C、矩形 D、正方形8. 菱形的两条对角线的分别为60cm和80cm,那么边长是( )A、100cm B、80cm C、60cm D、50cm9. 等腰三角形的腰长为10,底长为12,则其底边上的高为( )A、13 B、8 C、25 D、6410. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用 , 表示直角三角形的两直角边( ),下列四个说法:
A、3和2 B、2和3 C、4和1 D、1和47. 顺次连接对角线相等的四边形的各边中点,所形成的四边形是( )A、平行四边形 B、菱形 C、矩形 D、正方形8. 菱形的两条对角线的分别为60cm和80cm,那么边长是( )A、100cm B、80cm C、60cm D、50cm9. 等腰三角形的腰长为10,底长为12,则其底边上的高为( )A、13 B、8 C、25 D、6410. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用 , 表示直角三角形的两直角边( ),下列四个说法: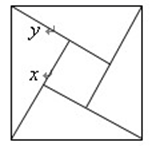
① ,② ,③ ,④ .
其中说法正确的是( )
A、①② B、①②③ C、①②④ D、①②③④二、填空题
-
11. 计算: =.12. 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为 .
 13. 已知实数a在数轴上的位置如图所示,则化简|a-1|- 的结果是.
13. 已知实数a在数轴上的位置如图所示,则化简|a-1|- 的结果是.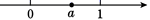 14. 观察以下几组勾股数,并寻找规律:
14. 观察以下几组勾股数,并寻找规律:①3,4,5;
②5,12,13;
③7,24,25;
④9,40,41,…
请你写出有以上规律的第⑤组勾股数:
15. 如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是(把所有正确结论的序号都填在横线上)(1)∠DCF= ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF 
三、解答题
-
16. 计算:(1)、( )÷(2)、( +1)2﹣ +(﹣2)217.(1)、当 时,求 的值;(2)、①x为何值时二次根式 的值是10?
②当x=▲时二次根式 有最小值.
18. 在平面直角坐标系中 (1)、在图中描出A(﹣2,﹣2),B(﹣8,6),C(2,1)(2)、连接AB、BC、AC,试判断△ABC的形状.19. 如图,在 中,对角线AC,BD相交于点O,E,F分别为BO,DO的中点,求证:AF∥CE.
(1)、在图中描出A(﹣2,﹣2),B(﹣8,6),C(2,1)(2)、连接AB、BC、AC,试判断△ABC的形状.19. 如图,在 中,对角线AC,BD相交于点O,E,F分别为BO,DO的中点,求证:AF∥CE. 20. 如图,P是正方形ABCD对角线BD上一点, , ,E、F分别为垂足,若 , ,求AP的长.
20. 如图,P是正方形ABCD对角线BD上一点, , ,E、F分别为垂足,若 , ,求AP的长. 21. 如图,将两张长为8,宽为4的矩形纸条交叉叠放,使一组对角的顶点重合,其重叠部分是四边形AGCH.
21. 如图,将两张长为8,宽为4的矩形纸条交叉叠放,使一组对角的顶点重合,其重叠部分是四边形AGCH. (1)、证明:四边形AGCH是菱形:(2)、求菱形AGCH的周长.22. 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)、证明:四边形AGCH是菱形:(2)、求菱形AGCH的周长.22. 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.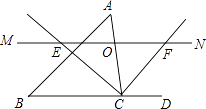 (1)、求证:OE=OF;(2)、若CE=12,CF=5,求OC的长;(3)、当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.23. 如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.
(1)、求证:OE=OF;(2)、若CE=12,CF=5,求OC的长;(3)、当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.23. 如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H. (1)、猜想四边形EFGH的形状,直接回答,不必说明理由;(2)、当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;
(1)、猜想四边形EFGH的形状,直接回答,不必说明理由;(2)、当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由; (3)、如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.
(3)、如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.