河南省南阳市宛城区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2021-05-08 类型:期中考试
一、单选题
-
1. 下列式子中是分式的是( )A、 B、 C、 D、2. 新冠病毒( )平均直径约为 (纳米).1米= 纳米, 用科学记数法可以表示为( )A、 B、 C、 D、3. 某种消毒液自年初以来,在库存为 的情况下,日销售量与产量持平,自2月底以来,需求量猛增,在生产能力不变的情况下,消毒液一度脱销.下图表示年初至脱销期间,时间t与库存量y之间函数关系的图象是( )A、
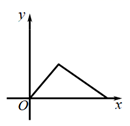 B、
B、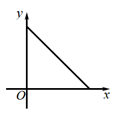 C、
C、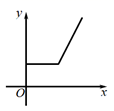 D、
D、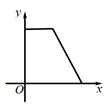 4. 化简 的结果为( )A、 B、 C、 D、5. 如图直线 与双曲线 相交于 两点,则不等式 的解集是( )
4. 化简 的结果为( )A、 B、 C、 D、5. 如图直线 与双曲线 相交于 两点,则不等式 的解集是( )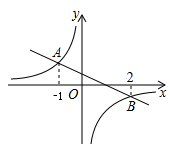 A、 或 B、 或 C、 或 D、 或6. 若 的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A、 B、 C、 D、7. 函数 与 在同一坐标系中的图象可能是( )A、
A、 或 B、 或 C、 或 D、 或6. 若 的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A、 B、 C、 D、7. 函数 与 在同一坐标系中的图象可能是( )A、 B、
B、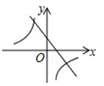 C、
C、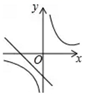 D、
D、 8. 根据如图所示的程序计算函数y的值,若输入的x值是﹣1或4时,输出的y值相等,则m的值是( )
8. 根据如图所示的程序计算函数y的值,若输入的x值是﹣1或4时,输出的y值相等,则m的值是( )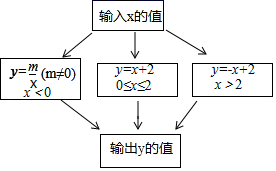 A、﹣1 B、1 C、﹣2 D、29. 如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1 , 第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn , 则P2020的坐标是( )
A、﹣1 B、1 C、﹣2 D、29. 如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1 , 第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn , 则P2020的坐标是( )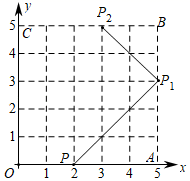 A、(5,3) B、(3,5) C、(0,2) D、(2,0)10. 一条公路旁依次有 三个村庄,甲乙两人骑自行车分别从 村、 村同时出发前往 村,甲乙之间的距离 与骑行时间 之间的函数关系如图所示,下列结论:① 两村相距10 ;②出发1.25 后两人相遇;③甲每小时比乙多骑行8 ;④相遇后,乙又骑行了15 或65 时两人相距2 .其中正确的个数是( )
A、(5,3) B、(3,5) C、(0,2) D、(2,0)10. 一条公路旁依次有 三个村庄,甲乙两人骑自行车分别从 村、 村同时出发前往 村,甲乙之间的距离 与骑行时间 之间的函数关系如图所示,下列结论:① 两村相距10 ;②出发1.25 后两人相遇;③甲每小时比乙多骑行8 ;④相遇后,乙又骑行了15 或65 时两人相距2 .其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 计算: .12. 若一个等腰三角形的周长是16,则其底边长y与腰长x之间的函数关系式是.(要求注明自变量x的取值范围).13. 化简: .14. 如图,过x轴正半轴上任意一点P作x轴的垂线,分别与反比例函数 和 的图象交于点A和点B.若点C是y轴上任意一点,则 的面积为.
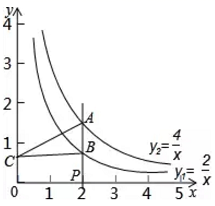 15. 如果关于x的方程 2无解,则a的值为.
15. 如果关于x的方程 2无解,则a的值为.三、解答题
-
16. 解方程: .17. 化简式子( 1) ,并在﹣2,﹣1,0,1,2中选取一个合适的数作为a的值代入求值.18. 已知一次函数 的图象与反比例函数 的图象交于点A,与x轴交于点 ,若 , .
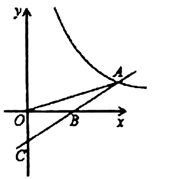 (1)、求反比例函数的解析式:(2)、若点P为x轴上一动点,当 是等腰三角形时,直接写出点P的坐标.19. 新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?20. 如图,已知直线 经过点 和 ,分别与x轴、y轴交于A、B两点.
(1)、求反比例函数的解析式:(2)、若点P为x轴上一动点,当 是等腰三角形时,直接写出点P的坐标.19. 新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?20. 如图,已知直线 经过点 和 ,分别与x轴、y轴交于A、B两点.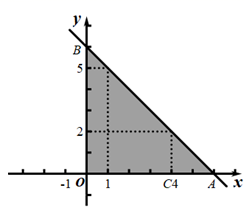 (1)、求直线 的解析式:(2)、若把横、纵坐标均为整数的点称为格点,则图中阴影部分(不包括边界)所含格点的个数有个;(3)、作出点 关于直线 的对称点D,则点D的坐标为;(4)、若在直线 和y轴上分别存在一点 使 的周长最短,请在图中标出点 (不写作法,保留痕迹).21. 春节前小明花1200元从市场购进批发价分别为每箱30元与50元的A、B两种水果进行销售,分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.(1)、求y关于x的函数表达式;(2)、若要求购进A水果的数量不少于B水果的数量,则应该如何分配购进A、B水果的数量并全部售出才能获得最大利润,此时最大利润是多少?22. 问题呈现:我们知道反比例函数y= (x>0)的图象是双曲线,那么函数y= +n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y= (x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
(1)、求直线 的解析式:(2)、若把横、纵坐标均为整数的点称为格点,则图中阴影部分(不包括边界)所含格点的个数有个;(3)、作出点 关于直线 的对称点D,则点D的坐标为;(4)、若在直线 和y轴上分别存在一点 使 的周长最短,请在图中标出点 (不写作法,保留痕迹).21. 春节前小明花1200元从市场购进批发价分别为每箱30元与50元的A、B两种水果进行销售,分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.(1)、求y关于x的函数表达式;(2)、若要求购进A水果的数量不少于B水果的数量,则应该如何分配购进A、B水果的数量并全部售出才能获得最大利润,此时最大利润是多少?22. 问题呈现:我们知道反比例函数y= (x>0)的图象是双曲线,那么函数y= +n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y= (x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……探索思考:我们可以借鉴以前研究函数的方法,首先探索函数y= 的图象.
(1)、填写下表,并画出函数y= 的图象.①列表:
x
…
﹣5
﹣3
﹣2
0
1
3
…
y
…
…
②描点并连线.
(2)、观察图象,写出该函数图象的两条不同类型的特征:①②;
理解运用:函数y= 的图象是由函数y= 的图象向平移个单位,其对称中心的坐标为.
灵活应用:根据上述画函数图象的经验,想一想函数y= +2的图象大致位置,并根据图象指出,当x满足时,y≥3.
23. 如图,直线 与x轴、y轴分别交于 两点, 于点M,点P为直线l上不与点 重合的一个动点.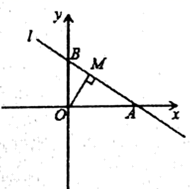 (1)、求线段 的长;(2)、当 的面积是6时,求点P的坐标;(3)、在y轴上是否存在点Q,使得以O、P、Q为顶点的三角形与 全等,若存在,请直接写出所有符合条件的点P的坐标,否则,说明理由.
(1)、求线段 的长;(2)、当 的面积是6时,求点P的坐标;(3)、在y轴上是否存在点Q,使得以O、P、Q为顶点的三角形与 全等,若存在,请直接写出所有符合条件的点P的坐标,否则,说明理由.