河南省南阳市唐河县2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2021-05-08 类型:期中考试
一、单选题
-
1. 若分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±12. 某种感冒病毒的直径是0.00000012米,将0.00000012用科学记数法可表示为( )A、12×10﹣8 B、1.2×10﹣8 C、1.2×10﹣7 D、0.12×10﹣73. 如图,在平面直角坐标系中,已知点 ,点 ,平移线段AB,使点A落在点 处,则点B的对应点 的坐标为( )
 A、 B、 C、 D、4. 如图,在平行四边形ABCD中,∠ADC的角平分线交边AB于点E,连接CE,若∠ADE=25°,∠BCE=15°,则∠BEC的度数为( )
A、 B、 C、 D、4. 如图,在平行四边形ABCD中,∠ADC的角平分线交边AB于点E,连接CE,若∠ADE=25°,∠BCE=15°,则∠BEC的度数为( ) A、115° B、120° C、125° D、130°5. 均匀的向一个容器内注水,在注水过程中,水面高度 与时间 的函数关系如图所示,则该容器是下列中的( )
A、115° B、120° C、125° D、130°5. 均匀的向一个容器内注水,在注水过程中,水面高度 与时间 的函数关系如图所示,则该容器是下列中的( ) A、
A、 B、
B、 C、
C、 D、
D、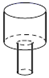 6. 若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )A、
6. 若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )A、 B、
B、 C、
C、 D、
D、 7. 为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用 万元购买甲型机器人和用 万元购买乙型机器人的台数相同,两型号机器人的单价和为 万元.若设甲型机器人每台 万元,根据题意,所列方程正确的是( )A、 B、 C、 D、8. 若点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)都在反比例函数 的图象上,则y1、y2、y3的大小关系是( )A、y1>y2>y3 B、y3>y2>y1 C、y2>y1>y3 D、y1>y3>y29. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法错误的是( )
7. 为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用 万元购买甲型机器人和用 万元购买乙型机器人的台数相同,两型号机器人的单价和为 万元.若设甲型机器人每台 万元,根据题意,所列方程正确的是( )A、 B、 C、 D、8. 若点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)都在反比例函数 的图象上,则y1、y2、y3的大小关系是( )A、y1>y2>y3 B、y3>y2>y1 C、y2>y1>y3 D、y1>y3>y29. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法错误的是( ) A、体育场离林茂家 B、体育场离文具店 C、林茂从体育场出发到文具店的平均速度是 D、林茂从文具店回家的平均速度是10. 如图:将 的对角线的交点与直角坐标系的原点重合,点 和 分别对应的D点,A点的坐标是( )
A、体育场离林茂家 B、体育场离文具店 C、林茂从体育场出发到文具店的平均速度是 D、林茂从文具店回家的平均速度是10. 如图:将 的对角线的交点与直角坐标系的原点重合,点 和 分别对应的D点,A点的坐标是( ) A、 和 B、 和 C、 和 D、 和
A、 和 B、 和 C、 和 D、 和二、填空题
-
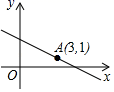
11. 计算: ﹣(-2020)0+|﹣5|﹣( )﹣1=.12. 如图,直线 经过点 ,当 时,x的取值范围为.
 13. 如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等于.
13. 如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等于. 14. 已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x= .15. 如图,平行于x轴的直线与函数 的图象分别相交于 两点,点A在点B的右侧,C为x轴上的一个动点,若 的面积为4,则 的值为。
14. 已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x= .15. 如图,平行于x轴的直线与函数 的图象分别相交于 两点,点A在点B的右侧,C为x轴上的一个动点,若 的面积为4,则 的值为。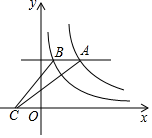
三、解答题
-
16. 计算下列各式:(1)、( ﹣1)÷ ;(2)、( ﹣1)÷ .17.(1)、解分式方程: + =1;(2)、先化简,再求值:先化简,再求值:( ﹣1)÷ 其中x的值从不等式组 的整数解中选取.18. 如图所示为某汽车行驶的路程S(km)与时间t(min)的函数关系图,观察图中所提供的信息解答下列问题:
 (1)、汽车在前9分钟内的平均速度是多少?(2)、汽车中途停了多长时间?(3)、当16≤t≤30时,求S与t的函数关系式?19. 如图,在 ABCD中,分别过 两点作对角线BD的垂线,垂足分别为M、N,连结AN、CM.
(1)、汽车在前9分钟内的平均速度是多少?(2)、汽车中途停了多长时间?(3)、当16≤t≤30时,求S与t的函数关系式?19. 如图,在 ABCD中,分别过 两点作对角线BD的垂线,垂足分别为M、N,连结AN、CM.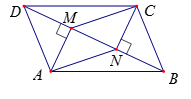
求证:
(1)、 ;(2)、四边形AMCN为平行四边形.20. 已知反比例函数y= (m为常数)的图象在第一、三象限.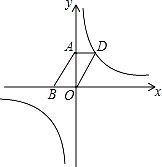 (1)、求m的取值范围;(2)、如图,若该反比例函数的图象经过▱ABOD的顶点D,点A,B的坐标分别为(0,3),(﹣2,0),求出该反比例函数的解析式;(3)、若E(x1 , y1),F(x2 , y2)都在该反比例函数的图象上,且x1>x2>0,则y1和y2有怎样的大小关系?21. 某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
(1)、求m的取值范围;(2)、如图,若该反比例函数的图象经过▱ABOD的顶点D,点A,B的坐标分别为(0,3),(﹣2,0),求出该反比例函数的解析式;(3)、若E(x1 , y1),F(x2 , y2)都在该反比例函数的图象上,且x1>x2>0,则y1和y2有怎样的大小关系?21. 某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:商品
甲
乙
进价(元/件)
售价(元/件)
200
100
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)、求甲、乙两种商品的进价是多少元?(2)、若超市销售甲、乙两种商品共50件,其中销售甲种商品为 件( ),设销售完50件甲、乙两种商品的总利润为 元,求 与 之间的函数关系式,并求出 的最小值.22. 在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质一一运用函数解决问题"的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义 .结合上面经历的学习过程,现在来解决下面的问题在函数 中,当 时, 当 时, (1)、求这个函数的表达式;(2)、在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质;(3)、已知函 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.23. 如图所示,一次函数y=kx+b的图象与反比例函数y= 的图象交于M、N两点.
(1)、求这个函数的表达式;(2)、在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质;(3)、已知函 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.23. 如图所示,一次函数y=kx+b的图象与反比例函数y= 的图象交于M、N两点. (1)、根据图中条件求出反比例函数和一次函数的解析式;(2)、连结OM、ON,求△MON的面积;(3)、根据图象,直接写出使一次函数的值大于反比例函数的值的x的取值范围.
(1)、根据图中条件求出反比例函数和一次函数的解析式;(2)、连结OM、ON,求△MON的面积;(3)、根据图象,直接写出使一次函数的值大于反比例函数的值的x的取值范围.