河南省南阳市邓州市2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2021-05-08 类型:期中考试
一、单选题
-
1. 下列式子中是分式的是( )A、 B、 C、 D、2. 若代数式 在实数范围内有意义,则实数 x 的取值范围是( )A、x > -1 B、x = -1 C、x≠0 D、x ≠-13. 2020年1月24日,中国疾控中心成功分离我国首株新型冠状病毒毒种,该毒种直径大约为90纳米(1纳米=0.000001毫米),数据“90纳米”用科学记数法表示为( )A、 毫米 B、 毫米 C、 毫米 D、 毫米4. 根据分式的基本性质,分式 可变形为( )A、 B、﹣ C、 D、5. 某公司为尽快给医院供应一批医用防护服,原计划x天生产1200套防护服,由于采用新技术,每天增加生产30套,因此提前2天完成任务,列出方程为( )A、 = ﹣30 B、 = ﹣30 C、 = ﹣30 D、 = ﹣306. 下列各曲线中不能表示y是x的函数是( )A、
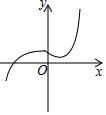 B、
B、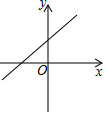 C、
C、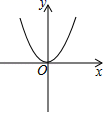 D、
D、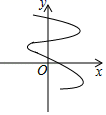 7. 若点P在一次函数 的图象上,则点P一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=118°,则∠BCE=( )
7. 若点P在一次函数 的图象上,则点P一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=118°,则∠BCE=( )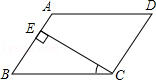 A、28° B、38° C、62° D、72°9. 如果反比例函数y= 的图象在每个象限内,y随着x的增大而增大,则m的最小整数值为( )A、﹣1 B、0 C、1 D、210. 如图,在平面直角坐标系中点A的坐标为(0,6),点B的坐标为(﹣ ,5),将△AOB沿x轴向左平移得到△A′O′B′,点A的对应点A′落在直线y=﹣ x上,则点B的对应点B′的坐标为( )
A、28° B、38° C、62° D、72°9. 如果反比例函数y= 的图象在每个象限内,y随着x的增大而增大,则m的最小整数值为( )A、﹣1 B、0 C、1 D、210. 如图,在平面直角坐标系中点A的坐标为(0,6),点B的坐标为(﹣ ,5),将△AOB沿x轴向左平移得到△A′O′B′,点A的对应点A′落在直线y=﹣ x上,则点B的对应点B′的坐标为( )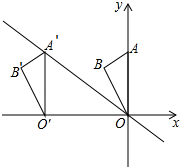 A、(﹣8,6) B、(﹣ ,5) C、(﹣ ,5) D、(﹣8,5)
A、(﹣8,6) B、(﹣ ,5) C、(﹣ ,5) D、(﹣8,5)二、填空题
-
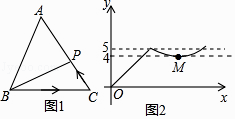
11. 计算:(-3)0+3-1=.12. 关于x的分式方程 有增根,则m的值为 .13. 若点A(1,y1)和点B(2,y2)在反比例函数y=﹣ 的图象上,则y1与y2的大小关系是.14. 如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 .
 15. 如图,在▱ABCD中,AB=3 ,BC=10,∠A=45°,点E是边AD上一动点,将△AEB沿直线BE折叠,得到△FEB,设BF与AD交于点M,当BF与▱ABCD的一边垂直时,DM的长为.
15. 如图,在▱ABCD中,AB=3 ,BC=10,∠A=45°,点E是边AD上一动点,将△AEB沿直线BE折叠,得到△FEB,设BF与AD交于点M,当BF与▱ABCD的一边垂直时,DM的长为.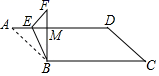
三、解答题
-
16. 先化简,再求值: ,其中x的值从不等式组 的整数解中选取.17. 小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
 (1)、小明家到学校的路程是多少米?(2)、在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?(3)、小明在书店停留了多少分钟?(4)、本次上学途中,小明一共行驶了多少米?一共用了多少分钟?18. 如图,点E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)、小明家到学校的路程是多少米?(2)、在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?(3)、小明在书店停留了多少分钟?(4)、本次上学途中,小明一共行驶了多少米?一共用了多少分钟?18. 如图,点E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.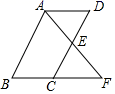 (1)、求证:△ADE≌△FCE.(2)、若AB=8,BC=5,则EF的长为时,AB⊥AF.19. 如图,点 , 在反比例函数 的图象上,作 轴于点C.
(1)、求证:△ADE≌△FCE.(2)、若AB=8,BC=5,则EF的长为时,AB⊥AF.19. 如图,点 , 在反比例函数 的图象上,作 轴于点C.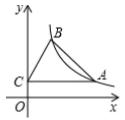 (1)、求反比例函数的表达式;(2)、若 的面积为 ,求点B的坐标.20. 为及时救治新冠肺炎重症患者,某医院需购买A、B两种型号的呼吸机.已知购买一台A型呼吸机需6万元,购买一台B型呼吸机需4万元,该医院准备投入资金y万元,全部用于购进35台这两种型号的呼吸机,设购进A型呼吸机x台.(1)、求y关于x的函数关系式;(2)、若购进B型呼吸机的数量不超过A型呼吸机数量的2倍,则该医院至少需要投入资金多少万元?21. 我们经历了“确定函数的表达式﹣利用函数图象研究其性质﹣运用函数解决问题”的学习过程在画函数图象时,我们通过描点的方法画出了所学的函数图象同时,我们也学习了绝对值的意义:|a|= ,结合上面经历的学习过程,解决下面问题:
(1)、求反比例函数的表达式;(2)、若 的面积为 ,求点B的坐标.20. 为及时救治新冠肺炎重症患者,某医院需购买A、B两种型号的呼吸机.已知购买一台A型呼吸机需6万元,购买一台B型呼吸机需4万元,该医院准备投入资金y万元,全部用于购进35台这两种型号的呼吸机,设购进A型呼吸机x台.(1)、求y关于x的函数关系式;(2)、若购进B型呼吸机的数量不超过A型呼吸机数量的2倍,则该医院至少需要投入资金多少万元?21. 我们经历了“确定函数的表达式﹣利用函数图象研究其性质﹣运用函数解决问题”的学习过程在画函数图象时,我们通过描点的方法画出了所学的函数图象同时,我们也学习了绝对值的意义:|a|= ,结合上面经历的学习过程,解决下面问题: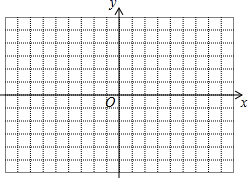 (1)、若一次函数y=kx+b的图象分别经过点A(﹣1,1),B(2,2),请求出此函数表达式;(2)、在给出的平面直角坐标系中,直接画出函数y=|x|和y=kx+b的图象;(3)、根据这两个函数图象直接写出不等式|x|≤kx+b的解集.22. 在△ABC中,AB=AC,点P为△ABC所在平面内一点过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
(1)、若一次函数y=kx+b的图象分别经过点A(﹣1,1),B(2,2),请求出此函数表达式;(2)、在给出的平面直角坐标系中,直接画出函数y=|x|和y=kx+b的图象;(3)、根据这两个函数图象直接写出不等式|x|≤kx+b的解集.22. 在△ABC中,AB=AC,点P为△ABC所在平面内一点过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.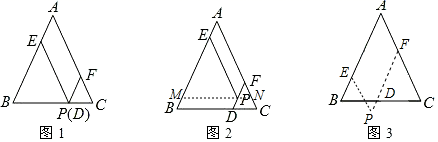 (1)、观察猜想
(1)、观察猜想如图1,当点P在BC边上时,此时点P、D重合,试猜想PD,PE,PF与AB的数量关系:.
(2)、类比探究如图2,当点P在△ABC内时,过点P作MN∥BC交AB于点M,交AC于点N,试写出PD,PE,PF与AB的数量关系,并加以证明.
(3)、解决问题如图3,当点P在△ABC外时,若AB=6,PD=1,请直接写出平行四边形PEAF的周长.
23. 如图,A点的纵坐标为3,过A点的一次函数图象与正比例函数y=2x的图象相交于点B. (1)、求该一次函数的表达式;(2)、若点P为第一象限内直线AB上的一动点,设点P的横坐标为m,过点P作x轴的垂线交正比例函数图象于点Q,交x轴于点M.
(1)、求该一次函数的表达式;(2)、若点P为第一象限内直线AB上的一动点,设点P的横坐标为m,过点P作x轴的垂线交正比例函数图象于点Q,交x轴于点M.①当△AOB≌△PQB时,求线段PM的长.
②当线段PQ= AO时,请直接写出点P的坐标.