四川省达州市2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期：2021-05-08 类型：期中考试
一、选择题(本大题共10小题、每小题5分，共 50分)
-
1. 若关于x的一元一次不等式组无解 ，则a的取值范围是（ ）A、a>1 B、a≥1 C、a＜-1 D、a≤-12. 等腰三角形的一个角是 50°，则它的底角的度数为（ ）A、50° B、50°或 80° C、50°或 65° D、65°3. 若a<b，则下列不等式不一定成立的是（ ）A、a+2<b+2 B、2a<2b C、 D、a2＜b24. 如图，在平面直角坐标系中，点B，C，E在y轴上，Rt△ABC经过变换得到Rt△ODE，若点C的坐标为(0，1)，AC=2，则这种变换可以是（ ）
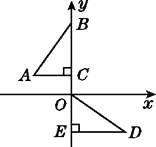A、△ABC绕点C顺时针旋转90°，再向下平移3个单位长度 B、△ABC绕点C顺时针旋转90°，再向下平移1个单位长度 C、△ABC绕点C逆时针旋转90°，再向下平移1个单位长度 D、△ABC绕点C逆时针旋转90°，再向下平移3个单位长度5. 以下命题中，真命题是（ ）A、两条直线只有一个交点 B、同位角相等 C、两边和一角对应相等的两个三角形全等 D、等腰三角形底边中点到两腰的距离相等6. 如图，在△ABC中，AB=AC，BD 平分∠ABC 交AC 平点D，AE∥BD 交CB 的延长线于点E。若∠E=35°，则∠BAC 的度数为（ ）
A、40° B、45° C、60° D、70°7. 如图，在△ABC 中，∠ACB =90°，AD 平分∠BAC 交 BC 于D，DE 垂直平分AB交AB 于E。若 DE=0.5AD=1.5cm，则 BC=（ ）
A、3 cm B、7.5 cm C、6 cm D、4.5 cm8. 如图，在 Rt△ACB 中，∠C=90°， AD 平分∠CAB 交BC平D，DE ⊥AB 交AB于E，则下列结论中不正确的是( ）
A、BD +ED=BC B、DE 平分∠ADB C、AD 平分∠EDC D、ED+AC>AD9. 若△ABC 的边 BC 的垂直平分线经过顶点 A，与 BC 相交于点D，且AB =2AD，则△ABC 中必有一个内角的度数为（ ），A、45° B、60° C、90° D、120°10. 如图，在△ABC 中，∠BAC = 90°，将△ABP 绕点 A 逆时针旋转后，能与△ACP'重合.如果 AP=3，那么 PP’的长等于（ ）
A、3 B、 C、 D、不能确定二、填空題(本大题共6小题，每小题5分，共30分)
-
11. 写出一个解集为x＞1的一元一次不等式： ．12. 在等腰△ABC 中，AD⊥BC 交直线 BC 于点 D.若 AD=0.5BC，则△ABC 的顶角的度数为13. 如图，在△ABC 中，AB =AC，AB 的垂直平分线交边 AB 手点D，交边 AC 于点E，连接 BE.若△ABC 与△EBC 的周长分别是 40 cm，24 cm，则 AB =cm.
14. 如图，在△ABC 中，∠B =115°，AC 边的垂直平分线 DE 交边 AB 于 D，且∠ACD：∠BCD =5：3，则∠ACB=.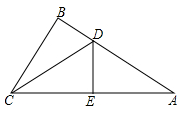
15. 如图，D是等边△ABC 的边 AC 的中点，点 E 在 BC 的延长线上，且 CE=CD.若S△ABC= cm2 ， 则△BDE 的周长是 .
16. 已知△ABC 的三边之和为m，S△ABC=S，则它的内心到各边的距离均为.三、解答题(本大题共10小题,共70分)
-
17. 解不等式组 ，并求出这个不等式组的整数解.18. 解不等式 2(x +1)-1≥3x+2并把它的解集在数轴上表示出来.19.
如图，在等边△ABC中，D是边AC上一点，连接BD．将△BCD绕点B逆时针旋转60°得到△BAE，连接ED．若BC=10，BD=9，求△AED的周长．
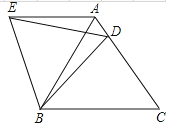20. 如图，在△ABC 中，∠BAC =80°，AB、AC 的垂直平分线分别与BC 交于 D、E，求∠EAD 的度数。
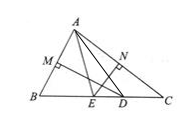21. 如图，在平面直角坐标系中，△ABC 各顶点的坐标分别是A（-2，-4)，B(O，-4)，C(1，-1).
( 1 )在图中画出△ABC 向左平移 3 个单位长度后得到的△A1 B1C1；
( 2 )在图中画出△ABC 绕原点O 逆时针旋转 90°后得到的△A2B2C2.
22. 某办公用品销售商店推出两种优惠方法：①购买1个书包，赠送1支水性笔；②购买书包和水性笔一律按 9 折优惠：书包每个定价 20 元，水性笔每支定价5元.小丽和同学需买4个书包，水性笔若干支(不少于4支).设购买费用为y元，购买水性笔x支.(1)、分别写出两种优惠方法下支付的费用 y(元)与所买水性笔支数 x(支)之间的函数关系式；(2)、通过对 x的取值情况进行分析，说明按哪种优惠方法购买更便宜；(3)、小丽和同学需买书包4个和水性笔12支，请你设计怎样购买更合算.23. 如图，AD 是∠BAC 的平分线，DE⊥AB 于E，DF ⊥AC于F，且BD =CD.求证：BE =CF.
24. 已知 M，N是线段AB的垂直平分线CD 上的两点.求证：∠MAN=∠MBN.
25. 如图，AD 是∠BAC 的平分线，DE⊥AB，DF ⊥AC，垂足分别是E，F，连接 EF：求证：AD 垂直平分EF.
26. 如图，在△ABC中，AB=AC=2，BC= ，∠BAC=90°，取一块含 45°角的直角三角尺，将直角顶点放在斜边 BC 的中点O处，一条直角边过点 A(如图①）.三角尺绕点 O顺时针方向旋转，使 90°角的两边与 Rt△ABC 的两边 AB，AC 分别相交于点E，F(如图②)、设 BE=x，CF =y.
(1)、探究：在图②中，线段 AE 与CF 有怎样的数量关系？请说明理由.(2)、求在上述旋转过程中γ与x的函数关系式，并写出x 的取值范围.(3)、若将直角三角尺 45°角的顶点放在斜边 BC 边的中点O 处，一条直角边过点 A(如图③).三角尺绕点 O 顺时针方向旋转，使 45°角的两边与 Rt△ABC 的两边 AB，AC 分别相交于点E，F(如图④).在三角尺绕点 O 旋转的过程中，△OEF 是否能成为等腰三角形?若能，直接写出△OEF 为等腰三角形时x 的值；若不能，请说明理由.