四川省眉山市青神县2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期:2021-05-08 类型:期中考试
一、精心选一选:(每题4分,共48分)
-
1. 当x=-1时,下列分式中有意义的是( )A、 B、 C、 D、2. 下列各式中,从左到右的变形正确的是( )A、 B、 C、 D、3. 把分式 中的x、y的值同时扩大为原来的2倍,则分式的值( )A、不变 B、扩大为原来的2倍 C、扩大为原来的4倍 D、缩小为原来的一半4. 下列分式中,最简分式是( )A、 B、 C、 D、5. 已知 , ,那么代数式 的值是( )A、2 B、 C、4 D、6. 某文化旅游节期间,几名同学包租一辆面包车前去游览,面包车的租金为180元,出发时又增加了两名同学,结果每个同学比原来少分摊了3元车费,设实际参加游览的同学共x人,则所列方程为( )A、 B、 C、 D、7. 在平面直角坐标系中,将点P(-3,2)向右平移3个单位得到点P1 , 则点P1关于x轴的对称点的坐标是:( )A、(0,-2) B、(0,2) C、(-6,2) D、(-6,-2)8. “六一”儿童节前夕,某部队战士到福利院慰问儿童,战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上),到达后接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战士们离营地的距离S与时间t之间函数关系的是( )A、
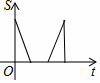 B、
B、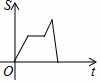 C、
C、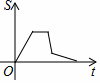 D、
D、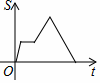 9. 已知反比例函数 (a≠0)的图象,在每一象限内, 的值随 值的增大而减小,则一次函数y -ax+a的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 一次函数y=ax-a与反比例函数y (a≠0)在同一坐标系中的图象可能是( )A、
9. 已知反比例函数 (a≠0)的图象,在每一象限内, 的值随 值的增大而减小,则一次函数y -ax+a的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 一次函数y=ax-a与反比例函数y (a≠0)在同一坐标系中的图象可能是( )A、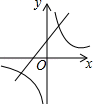 B、
B、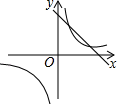 C、
C、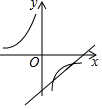 D、
D、 11. 已知点A(x1 , y1),B(x2 , y2)在反比例函数 的图象上,若y1<y2<0,则下列结论正确的是( )A、x1<x2<0 B、x2<x1<0 C、0<x1<x2 D、0<x2<x112. a是不为1的有理数,我们把 称为a的差倒数,如2 的差倒数为 ,-1的差倒数为 ,已知 , 是 的差倒数, 是 的差倒数, 是 的差倒数,以此类推, 的值是( )A、5 B、 C、 D、
11. 已知点A(x1 , y1),B(x2 , y2)在反比例函数 的图象上,若y1<y2<0,则下列结论正确的是( )A、x1<x2<0 B、x2<x1<0 C、0<x1<x2 D、0<x2<x112. a是不为1的有理数,我们把 称为a的差倒数,如2 的差倒数为 ,-1的差倒数为 ,已知 , 是 的差倒数, 是 的差倒数, 是 的差倒数,以此类推, 的值是( )A、5 B、 C、 D、二、耐心填一填(每题4分,共32分)
-
13. 如果分式 的值为零,那么x的值为。14. 某种芯片每个探针单元的面积为0.000 001 64cm2 , 0.000 001 64cm2用科学记数法表示为。15. 分式 、 、 的最简公分母是。16. 函数 中自变量 的取值范围是 。17. 如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,-1)和(-3,1),那么“卒”的坐标为。
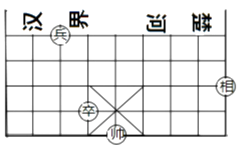 18. 若关于x的分式方程 的解为正数,则k的取值范围是 。19. 如图,点A在反比例函数 (x>0)的图象上,过点A作AB⊥x轴,垂足为B,交反比例函数 (x>0)的图象于点C.P为y轴上一点,连接PA,PC.则△APC的面积为.
18. 若关于x的分式方程 的解为正数,则k的取值范围是 。19. 如图,点A在反比例函数 (x>0)的图象上,过点A作AB⊥x轴,垂足为B,交反比例函数 (x>0)的图象于点C.P为y轴上一点,连接PA,PC.则△APC的面积为.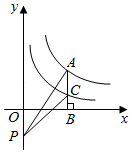 20. A、B两地相距240km , 甲货车从A地以40km/h的速度匀速前往B地,到达
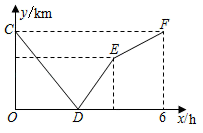
20. A、B两地相距240km , 甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的路程y(km)与甲货车出发的时间x(h)之间的函数关系如图中的折线CD—DE—EF所示,其中点C的坐标是(0,240),点D的坐标是(2.4,0),则点E 的坐标是。
三、细心算一算(每题7分,共28分)
-
21. 计算: .22. 化简: ,23. 先化简 ,再从-1,0,1中选择合适的x值代入求值.24. 解分式方程:
四、用心做一做(每题9分,共18分)
-
25. 某社区拟建A , B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米.建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元.用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的 .(1)、求每个A,B类摊位占地面积各为多少平方米?(2)、该社区拟建A,B两类摊位共90个,且B类摊位的数量不少于A类摊位数量的3倍.求建造这90个摊位的最大费用.26. 如图,已知过点B(1,0)的直线l1与直线 : 相交于点P(-1,a).
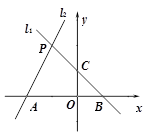 (1)、求直线l1的解析式;(2)、求四边形PAOC的面积
(1)、求直线l1的解析式;(2)、求四边形PAOC的面积五、大显身手(每题12分,共24分)
-
27. 小东到学校参加毕业晚会演出,到学校时发现演出道具还放在家中,此时距毕业晚会开始还有25分钟,于是立即步行回家.同时,他父亲从家里出发骑自行车以他3倍的速度给他送道具,两人在途中相遇,相遇后,小东父亲立即骑自行车以原来的速度载小东返回学校.图中线段AB、OB表示相遇前(含相遇)父亲送道具、小东取道具过程中,各自离学校的路程S(米)与所用时间t分)之间的函数关系,结合图象解答下列问题.
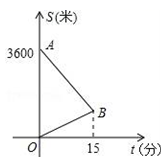 (1)、求点B坐标;(2)、求AB直线的解析式;(3)、小东能否在毕业晚会开始前到达学校?28. 如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数 图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)、求点B坐标;(2)、求AB直线的解析式;(3)、小东能否在毕业晚会开始前到达学校?28. 如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数 图象与BC交于点D,与AB交于点E,其中D(1,3).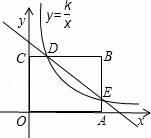 (1)、求反比例函数的解析式及E点的坐标;(2)、求直线DE的解析式;(3)、若矩形OABC对角线的交点为F(2, ),作FG⊥x轴交直线DE于点G.
(1)、求反比例函数的解析式及E点的坐标;(2)、求直线DE的解析式;(3)、若矩形OABC对角线的交点为F(2, ),作FG⊥x轴交直线DE于点G.①请判断点F是否在此反比例函数 的图象上,并说明理由;
②求FG的长度.