湖北省武汉市江岸区2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-05-08 类型：期中考试

进入出卷网下载

一、单选题

1. 化简 $\sqrt{25}$ 的结果为（）

A、±5 B、25 C、﹣5 D、5

查看试题解析
2. 若代数式 $\sqrt{x - 4}$ 有意义，则x的取值范围是（）

A、x≥4 B、x=4 C、x≤4 D、x≠4

查看试题解析
3. 在下列由线段a，b，c的长为三边的三角形中，不能构成直角三角形的是（）

A、a＝4，b＝5，c＝6 B、a＝12，b＝5，c＝13 C、a＝6，b＝8，c＝10 D、a＝7，b＝24，c＝25

查看试题解析
4. 下列说法错误的是（）

A、平行四边形的对角线互相平分 B、矩形的对角线相等 C、直角三角形斜边上的中线等于斜边的一半 D、对角线互相垂直的四边形是菱形

查看试题解析
5. 下列二次根式中，与 $\sqrt{6}$ 是同类二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{18}$ C、 $\sqrt{24}$ D、 $\sqrt{30}$

查看试题解析
6. 如图，已知平行四边形 $A B C D$ 中， $∠ B = 4 ∠ A$ ，则 $∠ C =$ （）

A、18° B、36° C、72° D、144°

查看试题解析
7. 如图，小明将一张长为 $20 cm$ ，宽为 $15 cm$ 的长方形纸 $(A E > D E)$ 剪去了一角，量得 $A B = 3 cm$ ， $C D = 4 cm$ ，则 $BC$ 长为（）

A、 $20 cm$ B、 $16 cm$ C、 $12 cm$ D、 $5 cm$

查看试题解析
8. 如图，在矩形ABCD中，AB＝8，BC＝4.将矩形沿AC折叠，CD′与AB交于点F，则AF：BF的值为（）

A、2 B、 $\frac{5}{3}$ C、 $\frac{5}{4}$ D、 $\sqrt{3}$

查看试题解析
9. 如图，在矩形ABCD中，AB=7，AD=5，对角线BD上的一动点，以E为直角顶点，AE为直角边做等腰Rt△AEF，（E，F按逆时针方向排列），当点E从点D运动到点B时，点F的运动路径长是（）

A、12 B、 $2 \sqrt{37}$ C、18 D、 $2 \sqrt{35}$

查看试题解析
10. 如图，在▱ABCD中，AD＝2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中：①∠DCF＝ $\frac{1}{2}$ ∠BCD；②EF＝CF；③S_△BEC＜2S_△CEF；④∠DFE＝4∠AEF.一定成立的有（）个.

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 计算： $(\sqrt{3} + 1) (\sqrt{3} - 1)$ =.

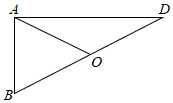
查看试题解析
12. 如图，Rt△DAB，∠DAB=90°，∠D=36°，O为DB中点，则∠BAO=.

查看试题解析
13. 等边三角形的边长是8，这个三角形的面积为 .

查看试题解析
14. 如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=6，AD=8，则四边形ABOM的周长为.

查看试题解析
15. 菱形ABCD的周长为24，∠ABC=60°，以AB为腰在菱形外作底角为45°的等腰△ABE，连结AC，CE，则△ACE的面积为.

查看试题解析
16. 已知a，b均为正数，且 $a + b = 8$ ，求 $\sqrt{a^{2} + 9} + \sqrt{b^{2} +9}$ 的最小值.

查看试题解析

三、解答题

17. 计算： $\sqrt{8} + \sqrt{32} - \sqrt{2}$ .

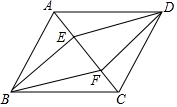
查看试题解析
18. 先化简，再求值： $a (3 - a) + (a + \sqrt{3}) (a - \sqrt{3})$ ，其中 $a = \sqrt{2} + 1$

查看试题解析
19. 如图，在平行四边形ABCD中，E、F是对角线AC上的两点，AE＝CF.求证：四边形BEDF是平行四边形.

查看试题解析
20. 如图是边长为 1 的小正方形网格，每个小正方形的顶点叫做格点，点A 、C均在格点上，且AC=5，请选择适当的格点，只用无刻度的直尺在网格中完成下列画图，并保留作图痕迹.

(1)、过点A画线段，使AB =5（点B在格点上），并且在AC上方；

(2)、在（1）的条件下，请画出∠BAC的角平分线；

(3)、在（1）的条件下，请画出以AB为一边的矩形，且满足矩形ANMB的面积=2△ABC的面积.

查看试题解析
21. 已知：如图，在平行四边形ABCD中，∠ABC的平分线交AD于点E，过点A作BE的垂线交BE于点F，交BC于点G，连接EG，CF.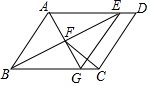

(1)、求证：四边形ABGE是菱形；

(2)、若∠ABC=60°，AB=4，AD=5，求CF的长.

查看试题解析
22. 如图1，菱形AEFG的两边AE、AG分别在菱形ABCD的边AB和AD上，且∠BAD=60°，连接CF；

(1)、求证： $\sqrt{3} D G = C F$ ；

(2)、如图2，将菱形AEFG绕点A进行顺时针旋转，在旋转过程中（1）中的结论是否发生变化？请说明理由.

查看试题解析
23. 对于任意正实数， ${(\sqrt{a} - \sqrt{b})}^{2} \geq 0$ ， $∴ a - 2 \sqrt{a b} + b \geq 0$ ， $∴ a + b \geq 2 \sqrt{a b}$ ，只有 $a = b$ 时，等号成立.结论：在 $a + b \geq 2 \sqrt{a b}$ (，均为正实数）中，若为定值，则 $a + b \geq 2 \sqrt{a b}$ ，只有当 $a = b$ 时，a+b有最小值 $2 \sqrt{p}$ .根据上述内容，回答下列问题：

(1)、初步探究：若 $n > 0$ ，只有当 $n =$ 时，有 $n + \frac{1}{n}$ 最小值；

(2)、深入思考：下面一组图是由4个全等的矩形围成的大正方形，中空部分是小正方形，矩形的长和宽分别为，试利用大正方形与四个矩形的面积的大小关系，验证 $a + b \geq 2 \sqrt{a b}$ ，并指出等号成立时的条件；

(3)、拓展延伸：如图，已知 $A (-6 ， 0)$ ， $B (0 ， -8)$ ，点是第一象限内的一个动点，过点向坐标轴作垂线，分别交轴和轴于，两点，矩形的面积始终为48，求四边形面积的最小值以及此时点的坐标.

查看试题解析
24. 已知平行四边形OABC，如图1，A（a，b），其中a，b满足 $\sqrt{a - 5} + b^{2} - 10 b + 25 = 0$ ，AB与y轴交于点D.

(1)、直接写出A点坐标；

(2)、如图2，点Q，P分别为x，y轴上的点，将△POQ沿PQ折叠使O恰好落在BA边上的E点，过E作EF//y轴交PQ于点T，交OC于点F.

①求证：TF=PD；

②若T（x，y），求x，y的关系式；

(3)、如图3，等腰Rt△MND，∠DNM=90°，连MA，S为MA的中点，连NS，MO，探究NS，MO的关系.

查看试题解析