湖北省武汉市2021年数学中考模拟试卷（4月）

试卷更新日期：2021-05-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数5的相反数是（）

A、 $\frac{1}{5}$ B、5 C、 $- \frac{1}{5}$ D、-5

查看试题解析
2. 式子 $\sqrt{x - 5}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x \geq - 5$ B、 $x \geq 5$ C、 $x \geq 0$ D、 $x \leq 2$

查看试题解析
3. 口袋中装有标号为1，2，3的三个小球，从口袋中摸出一个小球，则下列事件是随机事件的是（）

A、摸出的小球标号大于3 B、摸出的小球标号为3 C、摸出的小球标号小于1 D、摸出的小球标号不是5

查看试题解析
4. 在下列四个图案中，不是中心对称图形的是（）个

A、 B、 C、 D、

查看试题解析
5. 如图是由5个大小相同的小正方体摆成的几何体，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
6. 盒子里有 $3$ 张形状、大小、质地完全相同的卡片，上面分别标有数字1，2，3，从中随机抽出一张后不放回，再从中随机抽出一张，则两次抽出的卡片都是奇数的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、0

查看试题解析
7. 如图，平行于 $y$ 轴的直线分别交 $y = \frac{k_{1}}{x}$ 与 $y = \frac{k_{2}}{x}$ 的图象于点 $A$ ， $B$ ，点 $C$ 是 $y$ 轴上的点，则 $△ A B C$ 的面积为（）

A、 $k_{1} - k_{2}$ B、 $\frac{1}{2} (k_{1} - k_{2})$ C、 $k_{1} + k_{2}$ D、 $\frac{B E}{H E} = \frac{1}{2}$

查看试题解析
8. 甲、乙两地之间是一条直路，在全民健身活动中，赵明阳跑步从甲地往乙地，王浩月骑自行车从乙地往甲地，两人同时出发，王浩月先到达目的地，两人之间的距离 $s (km)$ 与运动时间 $t (h)$ 的函数关系大致如图所示，下列说法中错误的是（）.

A、两人出发1小时后相遇 B、赵明阳跑步的速度为 $8 km / h$ C、王浩月到达目的地时两人相距 $10 km$ D、王浩月比赵明阳提前 $1.5 h$ 到目的地

查看试题解析
9. 如图，在 $R t △ A O B$ 中， $∠ A O B = 90 ° ， O A = 3 ， O B = 4$ ，以点O为圆心，2为半径的圆与 $O B$ 交于点C，过点C作 $C D ⊥ O B$ 交 $A B$ 于点D，点P是边 $O A$ 上的动点.当 $P C + P D$ 最小时， $O P$ 的长为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、1 D、 $\frac{3}{2}$

查看试题解析
10. 如图，在平面直角坐标系中，点 $P_{1}$ 的坐标为 $(\frac{\sqrt{2}}{2} ， \frac{\sqrt{2}}{2})$ ，将线段 $O P_{1}$ 绕点 $O$ 按顺时针方向旋转 $45 °$ ，再将其长度伸长为 $O P_{1}$ 的2倍，得到线段 $O P_{2}$ ；又将线段 $O P_{2}$ 绕点 $O$ 按顺时针方向旋转 $45 °$ ，长度伸长为 $O P_{2}$ 的2倍，得到线段 $O P_{3}$ ，如此下去，得到线段 $O P_{4} ， O P_{5} ， \dots ， O P_{n}$ （ $n$ 为正整数），则点 $P_{2020}$ 的坐标是（）

A、 $(0 ， - 2^{2019})$ B、 $(0 ， - 2^{2020})$ C、 $(- 2^{2020} ， 0)$ D、 $(- 2^{2021} ， 0)$

查看试题解析

二、填空题

11. 一组数据：6，3，3，3，5，5，这组数据的中位数是.

查看试题解析
12. 计算 $\frac{{(x + 4)}^{2}}{x^{2} - 16} - \frac{8}{x - 4} =$ .

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ 、 $E$ 分别是 $A B$ 和 $A B$ 延长线上的点，且 $A D = A C$ ， $B C = B E$ ，则 $∠ D C E$ 的度数为.

查看试题解析
14. 函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与 $x$ 轴交于点 $(2, 0)$ ，顶点坐标为 $(- 1, n)$ ，其中 $n > 0$ .以下结论正确的是.
① $a b c > 0$ ；②函数 $y = a x^{2} + b x + c (a \neq 0)$ 在 $x = 1$ 和 $x = - 2$ 处的函数值相等；③函数 $y = k x + 1$ 的图象与 $y = a x^{2} + b x + c (a \neq 0)$ 的函数图象总有两个不同交点；④函数 $y = a x^{2} + b x + c (a \neq 0)$ 在 $- 3 \leq x \leq 3$ 内既有最大值又有最小值.

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $B C = 16$ ， $E$ 为 $C D$ 上一点，将 $△ B C E$ 沿 $B E$ 折叠，使点 $C$ 正好落在 $A D$ 边上的 $F$ 处，作 $∠ A B F$ 的平分线交 $A D$ 于 $N$ ，交 $E F$ 的延长线于 $M$ ，若 $N F = \frac{1}{2} B C$ ，则 $A B$ 的长为 .

查看试题解析

三、解答题

16. 计算： $[{(2 a^{2})}^{3} - 3 a \cdot a^{5}] \div a^{3}$ .

查看试题解析
17. 如图，点B、C、E、F都在同一直线上， $A C$ 与DE的延长线交于点G， $∠ B = ∠ D E F$ ， $A C // D F$ ，求证： $∠ A = ∠ D$ .

查看试题解析
18. 2020年某月，某医院收治了200名“新冠肺炎”患者，根据政府决定，对患者进行免费治疗，图1是该院轻症、重症、危重三类患者的人数分布统计图（不完整），图2是这三类患者的人均治疗费用统计图，请回答下列问题：
各类患者人均治疗费用条形统计图

(1)、轻症患者的人数为人；

(2)、该院为治疗危重患者共花费万元；

(3)、所有患者的平均治疗费用是多少万元？

查看试题解析
19. 如图，在 $7 \times 7$ 的正方形网格中，A、B、D、E都是格点，点C为AB与网格线的交点，用无刻度的直尺按下列要求作图：

（ 1 ）过点A作 $A M ⊥ D E$ 于M；

（ 2 ）过点 $C$ 作 $A B$ 的垂线；

（ 3 ）作 $▱ C D E F$ .

查看试题解析
20. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，以 $A B$ 为直径作 $⊙ O$ ，点 $D$ 为 $A B$ 上一点，过 $D$ 作 $D E ⊥ A B$ 交 $B C$ 于 $F$ ，交过点 $C$ 的切线于 $E$ 点.

(1)、求证： $C E = E F$ ；

(2)、若 $\frac{B D}{B C} = \frac{1}{2}$ ， $C F = D F$ ，求 $s i n ∠ C E D$ 的值.

查看试题解析
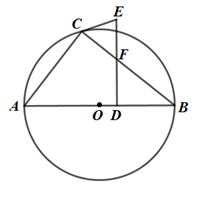21. 为了减少农产品库存，某板栗公司利用网络平台直播销售板栗，为提高大家购买的积极性，直播时板栗公司每天拿出 $2000$ 元作为红包发给购买者，已知该板栗的成本价格为 $6$ 元/千克，每天的销售量 $y$ （千克）与销售单价 $x$ （元/千克）满足关系式 $y = - 100 x + 5000$ ，销售单价不低于成本且不高于 $30$ 元/千克，设销售板栗日获利为 $W$ 元.

(1)、求日获利 $W$ 与销售单价 $x$ 的函数关系式；

(2)、当销售单价定为多少时，日获利最大？最大利润为多少元？

(3)、当 $W \geq 400000$ 时，网络平台将向公司收取 $a$ 元/千克 $(a < 4)$ 的相关费用，若此时日获利的最大值为 $42100$ 元，求 $a$ 的值.

查看试题解析
22. 如图

(1)、问题探究：如图1，在正方形 $A B C D$ 中，点 $E$ 、 $F$ 、 $G$ 分别是 $B C$ 、 $A B$ 、 $C D$ 上的点，且 $F G ⊥ A E$ ，求证： $F G = A E$ ；

(2)、类比应用：如图2，在矩形 $A B C D$ 中， $A B = n B C$ ， $F G ⊥ A E$ ，将矩形 $A B C D$ 沿 $F G$ 折叠使点 $A$ 落在 $E$ 点处，得到矩形 $F E P G$ .
①若点 $E$ 为 $B C$ 的中点，试探究 $F G$ 与 $A F$ 的数量关系；

②拓展延伸：连 $C P$ ，当 $n = \frac{3}{2}$ 时， $G F = 2 \sqrt{10}$ ， $t a n ∠ C G P = \frac{3}{4}$ ，求 $C P$ 的长.

查看试题解析
23. 已知抛物线 $y = a x^{2} + x + \frac{3}{4}$ 交 $x$ 轴于 $A$ 、 $B$ 两点（ $A$ 在 $B$ 左侧），直线 $y = k x + 3 k (k > \frac{1}{4})$ 经过点 $A$ ，交 $y$ 轴于 $M$ 点，交抛物线于另一点 $C$ .

(1)、求 $a$ 的值；

(2)、如图1，若 $P (0 ， n) (n > \frac{3}{4})$ ，直线 $P A$ 交抛物线于点 $E$ ，直线 $P B$ 交抛物线于 $F$ 点，且 $\frac{P A}{P E} = 3$ ，求 $\frac{P B}{P F}$ 的值；

(3)、如图2，点 $D (- 1 ， - 2)$ ，连 $C D$ 交抛物线于点 $Q$ ，连 $A Q$ 交 $y$ 轴于点 $N$ ，求 $O M \cdot O N$ 的值.

查看试题解析