福建省龙岩市上杭县初中毕业班2021年数学质量检查试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. -2021的相反数是( )A、2021 B、-2021 C、 D、2. 下面四个几何体中,主视图为三角形的是( )A、
 B、
B、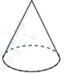 C、
C、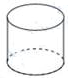 D、
D、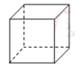 3. 已知 的周长为16,点 , , 分别为 三条边的中点,则 的周长为( )A、8 B、 C、16 D、44. 下列计算正确的是( )A、 B、 C、 D、5. 下列图形中,对称轴条数最多的是( )A、圆 B、正方形 C、等边三角形 D、平行四边形6. 我县3月份连续5天的最高气温分别为:19,20,22,20,24(单位:℃),则这组数据的众数和中位数分别为( )A、20,22 B、20,20 C、20,21 D、21,207. 把直线 向右平移2个单位后,所得直线的解析式为( )A、 B、 C、 D、8. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、9. 如图,三角形纸片ABC,点D是BC边上一点,连接AD,把 沿着AD翻折,得到 ,DE与AC交于点G,连接BE交AD于点F.若 , , , 的面积为2,则点F到BC的距离为( )
3. 已知 的周长为16,点 , , 分别为 三条边的中点,则 的周长为( )A、8 B、 C、16 D、44. 下列计算正确的是( )A、 B、 C、 D、5. 下列图形中,对称轴条数最多的是( )A、圆 B、正方形 C、等边三角形 D、平行四边形6. 我县3月份连续5天的最高气温分别为:19,20,22,20,24(单位:℃),则这组数据的众数和中位数分别为( )A、20,22 B、20,20 C、20,21 D、21,207. 把直线 向右平移2个单位后,所得直线的解析式为( )A、 B、 C、 D、8. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、9. 如图,三角形纸片ABC,点D是BC边上一点,连接AD,把 沿着AD翻折,得到 ,DE与AC交于点G,连接BE交AD于点F.若 , , , 的面积为2,则点F到BC的距离为( )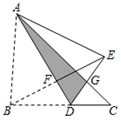 A、 B、 C、 D、10. 已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为-3,则 的值为( )A、3或4 B、0或4 C、0或7 D、7或3
A、 B、 C、 D、10. 已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为-3,则 的值为( )A、3或4 B、0或4 C、0或7 D、7或3二、填空题
-
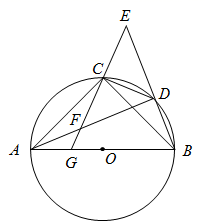
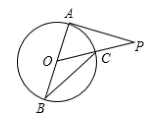
11. 计算: .12. 2020 年是新中国历史上极不平凡的一年.面对严峻复杂的国际形势、艰巨繁重的国内改革发展稳定任务特别是新冠肺炎疫情的严重冲击,以习近平同志为核心的党中央统揽全局,保持战略定力,准确判断形势,精心谋划部署,果断采取行动,付出艰苦努力,及时作出统筹疫情防控和经济社会发展的重大决策.根据《中华人民共和国2020年国民经济和社会发展统计公报》公布的数据,2020年全年国内生产总值达1010000亿余元,比上年增长2.3%.用科学记数法表示 1010000亿元为亿元.13. 如图,AB是 的直径,PA切 于点A , 线段PO交 于点C . 连接BC , 若 ,则 .
 14. 有三张大小、形状完全相同的卡片.卡片上分别写有数字1,2,3,从这三张卡片中随机先后不放回地抽取两张,则两次抽出数字之和为奇数的概率是.15. 如图,山顶上有一个信号塔 ,已知信号塔高 ,在山脚下点 处测得塔底 的仰角 ,塔顶 的仰角 ,则山高 m(点 , , 在同一条竖直线上,参考数据: , , ).
14. 有三张大小、形状完全相同的卡片.卡片上分别写有数字1,2,3,从这三张卡片中随机先后不放回地抽取两张,则两次抽出数字之和为奇数的概率是.15. 如图,山顶上有一个信号塔 ,已知信号塔高 ,在山脚下点 处测得塔底 的仰角 ,塔顶 的仰角 ,则山高 m(点 , , 在同一条竖直线上,参考数据: , , ).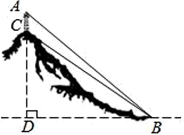 16. 如图,平面直角坐标系中,点 , 在 轴上,点 在 轴上,直线 交双曲线 第一象限于点 ,连接 , , ,若 , , ,则 的值是.
16. 如图,平面直角坐标系中,点 , 在 轴上,点 在 轴上,直线 交双曲线 第一象限于点 ,连接 , , ,若 , , ,则 的值是.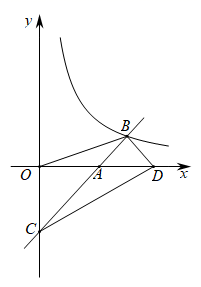
三、解答题
-
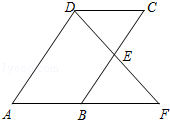
17. 解不等式组: .18. 如图,在平行四边形ABCD中,E为BC的中点,连接DE.延长DE交AB的延长线于点F.求证:AB=BF.
 19. 先化简,再求值: ,其中 .20. 将 绕点 逆时针旋转一个角度 得到 ,点 , 的对应点分别为 、 .
19. 先化简,再求值: ,其中 .20. 将 绕点 逆时针旋转一个角度 得到 ,点 , 的对应点分别为 、 .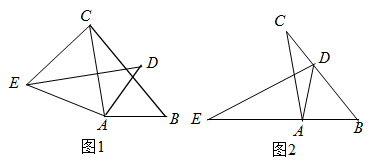 (1)、若 ,如图1,连接 ,试判断 的形状,并给以证明;(2)、若点 恰好落在 边上,如图2,且点 , , 在同一条直线上, ,求旋转角 的度数.21. 青少年学生要德智体美劳全面发展,坚持锻炼是提高身体素质的重要途径.为了解初三年级学生每周的课外锻炼情况,某校随机抽取初三年级若干名学生(其中女生20人),对他们一周参加课外锻炼的时间进行了调查,四舍五入处理后分男生,女生分别制作了不完整的统计表和统计图.已知一周课外锻炼2小时的女生人数占样本人数的16%,一周课外锻炼4小时的男女生人数相等.样本中女生的课外锻炼时间数据(单位:小时)为:0.9,1.3,1.7,3.2,1.8,2.2,3.9,2.2,2.4,3.2,4.2,3.2,3.3,1.9,2.2,3.8,3.9,4.1,4.3,2.3
(1)、若 ,如图1,连接 ,试判断 的形状,并给以证明;(2)、若点 恰好落在 边上,如图2,且点 , , 在同一条直线上, ,求旋转角 的度数.21. 青少年学生要德智体美劳全面发展,坚持锻炼是提高身体素质的重要途径.为了解初三年级学生每周的课外锻炼情况,某校随机抽取初三年级若干名学生(其中女生20人),对他们一周参加课外锻炼的时间进行了调查,四舍五入处理后分男生,女生分别制作了不完整的统计表和统计图.已知一周课外锻炼2小时的女生人数占样本人数的16%,一周课外锻炼4小时的男女生人数相等.样本中女生的课外锻炼时间数据(单位:小时)为:0.9,1.3,1.7,3.2,1.8,2.2,3.9,2.2,2.4,3.2,4.2,3.2,3.3,1.9,2.2,3.8,3.9,4.1,4.3,2.3女生一周课外锻炼时间频数分布表:
分组(四舍五入)
1小时
2小时
3小时
4小时
频数(学生人数)
2
4
男生一周课外锻炼时间频数分布直方图:
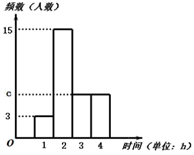 (1)、表中 , 直方图中 ;(2)、估算该校初三学生一周参加课外锻炼的平均时间.22. 如图, 中, , 是 的中点,点 在 上,且 .
(1)、表中 , 直方图中 ;(2)、估算该校初三学生一周参加课外锻炼的平均时间.22. 如图, 中, , 是 的中点,点 在 上,且 .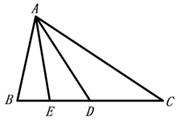 (1)、过点 作 的平行线 交射线 于点 ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、求证: .23. 去年在我县创建“国家文明县城”行动中,某社区计划将面积为 的一块空地进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的1.8倍,如果两队各自独立完成面积为 区域的绿化时,甲队比乙队少用4天.甲队每天绿化费用是1.05万元,乙队每天绿化费用为0.5万元.(1)、求甲、乙两工程队每天各能完成多少面积(单位: )的绿化;(2)、由于场地原因,两个工程队不能同时进场绿化施工,现在先由甲工程队绿化若干天,剩下的绿化工程由乙工程队完成,要求总工期不超过48天,问应如何安排甲、乙两个工程队的绿化天数才能使总绿化费用最少,最少费用是多少万元?
(1)、过点 作 的平行线 交射线 于点 ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、求证: .23. 去年在我县创建“国家文明县城”行动中,某社区计划将面积为 的一块空地进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的1.8倍,如果两队各自独立完成面积为 区域的绿化时,甲队比乙队少用4天.甲队每天绿化费用是1.05万元,乙队每天绿化费用为0.5万元.(1)、求甲、乙两工程队每天各能完成多少面积(单位: )的绿化;(2)、由于场地原因,两个工程队不能同时进场绿化施工,现在先由甲工程队绿化若干天,剩下的绿化工程由乙工程队完成,要求总工期不超过48天,问应如何安排甲、乙两个工程队的绿化天数才能使总绿化费用最少,最少费用是多少万元?