浙江省温州市平阳县2021年初中学业水平适应性考试数学试卷

试卷更新日期：2021-05-08 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{6}{17}$ 的相反数是（）

A、 $\frac{6}{17}$ B、 $\frac{17}{6}$ C、 $- \frac{6}{17}$ D、 $- \frac{17}{6}$

查看试题解析
2. 1938年出版的第一部中国现代数学词典《算学名词汇编》是温籍数学家姜立夫领导审定的，共收入7400多数学词汇，从而奠定了中国现代数学名词的基础.其中数据7400用科学记数法表示为（）

A、 $74 \times 10^{2}$ B、 $7.4 \times 10^{4}$ C、 $0.74 \times 10^{4}$ D、 $7.4 \times 10^{3}$

查看试题解析
3. 某物体如图所示，它的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 某校九年级学生中考体育选考项目组合情况的统计图如图所示，若九年级学生共有400人，则选择跳远、游泳、篮球项目组合的有（）

A、60人 B、80人 C、120人 D、140人

查看试题解析
5. 分式 $\frac{x + 3}{x - 2}$ 的值是零，则x的值为（）

A、2 B、3 C、 $- 2$ D、 $- 3$

查看试题解析
6. 已知现有的8瓶可乐中有2瓶已过了保质期，从这8瓶可乐中随机抽取1瓶，恰好取到已过了保质期的可乐的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{3}{4}$ C、 $\frac{1}{8}$ D、 $\frac{7}{8}$

查看试题解析
7. 已知反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象如图所示，当 $1 ⩽ x ⩽ 2$ 时，y的取值范围是（）

A、 $1 ⩽ y ⩽ 2$ B、 $0 ⩽ y ⩽ 4$ C、 $1 ⩽ y ⩽ 4$ D、 $2 ⩽ y ⩽ 4$

查看试题解析
8. 如图， $A ， B$ 两个物体分别在倾斜角为 $α ， β$ 的斜面上向上运动，物体A上升的高度比物体B上升的高度高（）

A、 $m \sin β - n \tan α$ B、 $m \sin β - \frac{n}{\tan α}$ C、 $\frac{m}{\sin β} - n \tan α$ D、 $\frac{m}{\sin β} - \frac{n}{\tan α}$

查看试题解析
9. 小慧在超市里买了一些物品，用一个长方体的箱子“打包”，这个箱子的尺寸如图1所示（其中 $b > a > c > 0$ ），售货员分别可按图2、图3、图4三种方法进行捆绑，设图2、图3、图4的捆绑绳长分别为 $l_{1} ， l_{2} ， l_{3}$ ，则 $l_{1} ， l_{2} ， l_{3}$ 的大小关系为（）

A、 $l_{1} > l_{3} > l_{2}$ B、 $l_{3} > l_{1} > l_{2}$ C、 $l_{1} > l_{2} > l_{3}$ D、 $l_{3} > l_{2} > l_{1}$

查看试题解析
10. 几千年来，在勾股定理的多种证明方法中，等面积法是典型的一种证法，清代数学家李锐运用这一方法借助三个正方形也证明了勾股定理.如图，四边形 $A B C D$ ，四边形 $D E F G$ ，四边形 $C G H I$ 均为正方形， $E F$ 交 $B G$ 于点 $L ， D G$ 交 $I H$ 于点K，点 $B ， L ， C ， G$ 在同条直线上，若 $S_{△ A D E} = 9$ ， $S_{△ G H K} = 4$ ，记四边形 $D E L C$ 的面积为 $S_{1}$ ，四边形 $C G K I$ 的面积为 $S_{2}$ ，则 $\frac{S_{1}}{S_{2}}$ 的值为（）

A、 $\frac{9}{4}$ B、 $\frac{17}{8}$ C、 $\frac{13}{6}$ D、 $\frac{3}{2}$

查看试题解析

二、填空题

11. 分解因式： $a^{2} - 4 a$ ＝．

查看试题解析
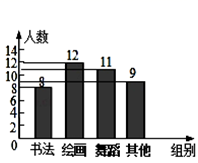
12. 不等式组 ${\begin{array}{l} \frac{x + 2}{3} \geq 1 \\ x - 1 < 5 \end{array}$ 的解为.

查看试题解析
13. 为了解在校学生参加课外兴趣小组活动情况，随机调查了40名学生，将结果绘制成了如图所示的统计图，则参加书法兴趣小组的频率是 .

查看试题解析
14. 已知扇形的半径为 $6 c m$ ，扇形的弧长为 $5 π c m$ ，则此扇形的圆心角是.

查看试题解析
15. 如图，菱形 $A B C D$ 的对角线 $A C ， B D$ 相交于点O，将菱形 $A B C D$ 绕点O按逆时针方向旋转 $90 °$ 得到菱形 $E F G H$ ，若两个菱形重叠部分八边形的周长为16， $∠ B A D = 60 °$ ，则 $H G$ 的长为.

查看试题解析
16. 图1是一种 $360 °$ 自动旋转农业灌溉摇臂喷枪.点P为喷水口，水雾喷出的路径可以近似看作抛物线 $y = - \frac{1}{50} x^{2} + \frac{3}{4} x + c$ 的一部分（如图2），已知 $\frac{O P}{O Q} = \frac{1}{20}$ ，则喷洒半径 $O Q$ 为米（喷枪长度忽略不计）；现有一块四边形 $A B C D$ 农出，它的四个顶点 $A ， B ， C ， D$ 恰好在 $⊙ O$ 上（如图3）， $B D = 25 \sqrt{15}$ 米， $\cos ∠ C = \frac{1}{4}$ .焊接一个底座支架可升高喷水口，如果喷水口上升时，水雾喷出的形状与原来相同，要使喷水区域覆盖整块四边形 $A B C D$ 农田，那么喷水口点P应至少升高米.

查看试题解析

三、解答题

17. 计算与化简

(1)、计算： ${(- 3)}^{2} - \sqrt{12} + {(4 + \sqrt{7})}^{0} - | - 5 |$ .

(2)、化简： ${(x + 3)}^{2} - (x + 2) (x - 2)$ .

查看试题解析
18. 如图，在四边形 $A B C D$ 中， $∠ B = 90 ° ， D A ⊥ A C$ ，点E在线段 $A C$ 上， $A B / / D E ， A C = D E$ .

(1)、求证： $△ A B C ≌ △ E A D$ .

(2)、连结 $C D$ ，当 $A C = 4 ， A B = 3$ ，求 $C D$ 的长.

查看试题解析

19. 4月7日是世界卫生日.某校在七、八年级共1000名学生中开展“爱国卫生”知识竞赛，从七、八年级学生中随机抽取20名学生的竞赛成绩（满分100分，80分及以上为优秀）进行整理和分析，绘制出如下统计表.

七，八年级抽取的学生的竞赛成绩统计表

成绩（分）	40	50	60	70	80	90	100
抽取的七年级人数（人）	1	2	1	7	5	3	1
抽取的八年级人数（人）	2	0	4	4	6	2	2

学校对平均数、中位数、众数、优秀率进行分析，绘制成如下统计表.

年级	平均数	中位数	众数	优秀率
七年级	73	a	70	$45 %$
八年级	73	b	c	d

根据以上信息，解答下列问题：

(1)、直接写出上述表中的

a

、

b

、

c

、

d

的值；

(2)、请你从平均数、中位数、众数、优秀率的角度进行分析，评价哪个年级的学生在知识竞赛中表现更加优异.

查看试题解析

20. 在 $6 \times 6$ 的正方形网格中，每个小正方形的边长都是1，线段 $A B$ 的两个端点都在格点上，请按下列要求作图，所作图形的顶点都在格点上.

(1)、在图1中画一个以 $A B$ 为斜边的 $Rt △ A B C$ ，且满足两直角边都是无理数.

(2)、在图2中画一个 $▱ A B C D$ ，且满足两条对角线互相垂直.

查看试题解析
21. 如图，在平面直角坐标系中，边长为4的正方形 $A B C D$ 的顶点A与原点重合，顶点 $B ， D$ 分别在x轴正半轴，y轴正半轴上，抛物线经过点 $B ， D ， E ， E$ 为 $C D$ 的中点.

(1)、求抛物线的函数表达式.

(2)、点P为抛物线上一点，向左平移与抛物线上点G重合，向下平移与线段 $B D$ 上点H重合，若 $P G = 2 P H$ ，求点P的坐标.

查看试题解析
22. 如图， $⊙ O$ 是矩形 $A B C D$ 的外接圆， $∠ A B C$ 的平分线分别交 $A C ， ⊙ O ， C D$ 的延长线于点 $E ， F ， G$ ，过点F作 $⊙ O$ 的切线 $F H$ ，交 $C G$ 于点H.

(1)、证明： $F H / / A C$ .

(2)、若 $\tan ∠ B A C = 3 ， O E = 2$ ，求 $F H$ 的长.

查看试题解析
23. 某超市销售 $A, B$ 两种饮料，A种饮料进价比B种饮料每瓶低2元，用500元进货A种饮料的数量与用600元进货B种饮料的数量相同.

(1)、求 $A, B$ 两种饮料平均每瓶的进价.

(2)、经市场调查表明，当A种饮料售价在11元到17元之间（含11元，17元）浮动时，每瓶售价每增加0.5元时，日均销售量减少20瓶；当售价为每瓶12元时，日均销售量为320瓶；B种饮料的日均毛利润m（元）与售价为n（元/瓶） $(12.5 ⩽ n ⩽ 18)$ 构成一次函数，部分数据如下表：（每瓶毛利润 $=$ 每瓶售价 $-$ 每瓶进价）

售价n（元/瓶）

18

17.5

16

…

日均毛利润m（元）

640

700

880

…

①当B种饮料的日均毛利润超过A种饮料的最大日均毛利润时，求n的取值范围.

②某日该超市B种饮料每瓶的售价比A种饮料高3元，售价均为整数，当A种饮料的售价定为每瓶多少元时，所得总毛利润最大？最大总毛利润是多少元？

查看试题解析
24. 如图，点 $E ， F$ 分别在矩形 $A B C D$ 的边 $B C ， A D$ 上， $B E = D F = 4 ， A F = 2$ ， $C D = 4 \sqrt{3}$ .点G为 $C F$ 上一点，连结 $B G$ 交 $A E$ 于 $H ， H E = 2 F G$ .点P从点H匀速运动到终点E，点Q在线段 $C G$ 上.记 $P H = x ， C Q = y$ ，满足 $y = k x + \frac{7}{2}$ （k为常数， $k \neq 0$ ）.

(1)、求证：四边形 $A E C F$ 是平行四边形.

(2)、求 $H E$ 的长.

(3)、在点P的运动过程中，当Q为 $C G$ 的中点时，点 $B ， P ， Q$ 在同一条直线上.
①求k的值.

②过点Q作 $Q R ⊥ B C$ 于点R，连结 $P Q ， P R$ ，当 $△ P Q R$ 为直角三角形时，求所有满足条件的 $P H$ 的长.

查看试题解析

售价n（元/瓶）	18	17.5	16	…
日均毛利润m（元）	640	700	880	…