浙江省温州市龙湾区2021年数学中考第一次适应性试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
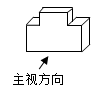
1. 数5, ,0,﹣3中最小的是( )A、5 B、 C、0 D、﹣32. 一个64位的量子计算机的数据处理速度约是目前世界上最快的“太湖之光”超级计算机的150000000000倍.其中数据150000000000用科学记数法表示为( )A、0.15× B、1.5× C、15× D、1.5×3. 某服务台如图所示,它的主视图为( )
 A、
A、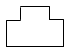 B、
B、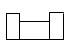 C、
C、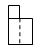 D、
D、 4. 温州2021年3月1日~7日的气温折线统计图如图所示,其中实线表示当日最高气温,虚线表示当日最低气温.由图可知,这一周中温差最小的是( )
4. 温州2021年3月1日~7日的气温折线统计图如图所示,其中实线表示当日最高气温,虚线表示当日最低气温.由图可知,这一周中温差最小的是( )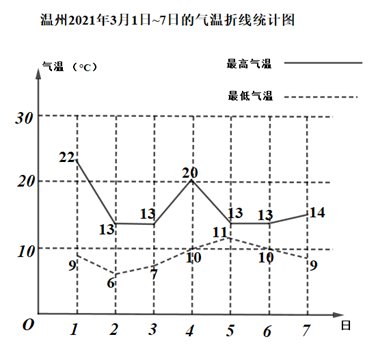 A、3月1日 B、3月4日 C、3月5日 D、3月7日5. 若分式 的值为0,则x的值是( )A、-3 B、-2 C、0 D、26. 甲、乙、丙、丁四名学生参加市中小学生运动会跳高项目预选赛,他们8次跳高的平均成绩及方差如表所示,要选一位成绩较好且稳定的运动员去参赛,应选运动员( )
A、3月1日 B、3月4日 C、3月5日 D、3月7日5. 若分式 的值为0,则x的值是( )A、-3 B、-2 C、0 D、26. 甲、乙、丙、丁四名学生参加市中小学生运动会跳高项目预选赛,他们8次跳高的平均成绩及方差如表所示,要选一位成绩较好且稳定的运动员去参赛,应选运动员( )甲
乙
丙
丁
(米)
1.7
1.75
1.75
1.72
S2(米2)
1
1.3
1
1.3
A、甲 B、乙 C、丙 D、丁7. 如图,在菱形ABCD中,E是对角线AC上的一点,过点E作FH AD,GI AB,点F,G,H,I分别在AB,BC,CD,DA上.若AC=a,∠B=60°,则图中阴影部分的周长为( )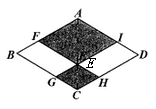 A、 B、4a C、 D、6a8. 某零件轴截面的示意图如图所示,它是关于直线m成轴对称的梯形,则大头直径D的长为( )
A、 B、4a C、 D、6a8. 某零件轴截面的示意图如图所示,它是关于直线m成轴对称的梯形,则大头直径D的长为( )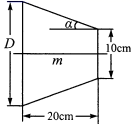 A、(10+ )厘米 B、(10 )厘米 C、(10+40sinα)厘米 D、(10+40tanα)厘米9. 如图,已知点P1为直线l:y=﹣2x+6上一点,先将点P1向下平移a个单位,再向右平移3个单位至点P2 , 然后再将点P2向下平移2个单位,向右平移b个单位至点P3.若点P3恰好落在直线l上,则a,b应满足的关系是( )
A、(10+ )厘米 B、(10 )厘米 C、(10+40sinα)厘米 D、(10+40tanα)厘米9. 如图,已知点P1为直线l:y=﹣2x+6上一点,先将点P1向下平移a个单位,再向右平移3个单位至点P2 , 然后再将点P2向下平移2个单位,向右平移b个单位至点P3.若点P3恰好落在直线l上,则a,b应满足的关系是( )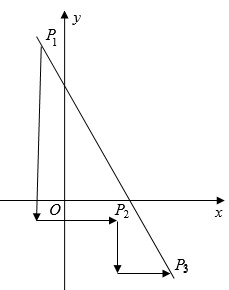 A、a﹣2b=4 B、b﹣2a=1 C、a+2b=8 D、2a+b=710. 如图,在Rt△ABC中,∠ACB=90°,分别以AB,BC,CA为直径作半圆围成两月牙形,过点C作DF AB分别交三个半圆于点D,E,F.若 ,AC+BC=15,则阴影部分的面积为( )
A、a﹣2b=4 B、b﹣2a=1 C、a+2b=8 D、2a+b=710. 如图,在Rt△ABC中,∠ACB=90°,分别以AB,BC,CA为直径作半圆围成两月牙形,过点C作DF AB分别交三个半圆于点D,E,F.若 ,AC+BC=15,则阴影部分的面积为( )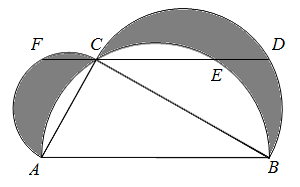 A、16 B、20 C、25 D、30
A、16 B、20 C、25 D、30二、填空题
-
11. 分解因式:x2﹣4= .
12. 在同一副扑克牌中抽取3张“黑桃”,1张“红桃”,4张“梅花”,将这8张牌背面朝上,从中任意抽取1张,是“黑桃”的概率为.13. 若扇形的圆心角为90°,半径为6,则该扇形的面积为.14. 不等式组 ,的解为.15. 如图,反比例函数 (k>0)在第一象限经过A,B两点.过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,BE⊥x轴于点E,连接AD,AB.若BD=4AC,△ADB的面积为9,则k的值为. 16. 如图1是护眼学习台灯,该台灯的活动示意图如图2所示.灯柱BC=6cm,灯臂AC绕着支点C可以旋转,灯罩呈圆弧形(即 和 ).在转动过程中,AD(EF)总是与桌面BH平行.当AC⊥BH时,AB=46cm,DM⊥MH,测得DM=37.5cm(点M在墙壁M上,且MH⊥BH);当灯臂AC转到CE位置时,FN⊥MH测得FN=13.5cm,则点E到桌面BH的距离为cm.若此时点C,F,M在同一条直线上, 的最低点到桌面BH的距离为35cm,则EF所在圆的半径为cm.
16. 如图1是护眼学习台灯,该台灯的活动示意图如图2所示.灯柱BC=6cm,灯臂AC绕着支点C可以旋转,灯罩呈圆弧形(即 和 ).在转动过程中,AD(EF)总是与桌面BH平行.当AC⊥BH时,AB=46cm,DM⊥MH,测得DM=37.5cm(点M在墙壁M上,且MH⊥BH);当灯臂AC转到CE位置时,FN⊥MH测得FN=13.5cm,则点E到桌面BH的距离为cm.若此时点C,F,M在同一条直线上, 的最低点到桌面BH的距离为35cm,则EF所在圆的半径为cm.
三、解答题
-
17. 计算与化简(1)、计算: ﹣( ﹣1)0+|﹣3|﹣( )﹣1;(2)、化简:a(a+4)﹣(a﹣2)2.18. 如图,点A,C,D,E在同一条直线上,BC⊥AE,FD⊥AE,AB EF,且AB=EF.
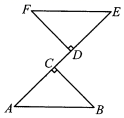 (1)、求证:△ABC≌△EFD.(2)、若AE=8,CD=2,∠A=45°,求AB的长.19. 在学校组织的知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为10分,9分,8分,7分,学校将八年级一班和二班参赛人员的成绩整理并绘制成如下的统计图.
(1)、求证:△ABC≌△EFD.(2)、若AE=8,CD=2,∠A=45°,求AB的长.19. 在学校组织的知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为10分,9分,8分,7分,学校将八年级一班和二班参赛人员的成绩整理并绘制成如下的统计图. (1)、分别求出此次比赛中两个班的平均成绩.(2)、从两个班成绩的平均数、中位数和众数的角度进行分析,你认为哪个班的成绩更好?20. 如图,∠ACB在6×6方格中,点A,B,C在格点上,按要求画图:
(1)、分别求出此次比赛中两个班的平均成绩.(2)、从两个班成绩的平均数、中位数和众数的角度进行分析,你认为哪个班的成绩更好?20. 如图,∠ACB在6×6方格中,点A,B,C在格点上,按要求画图: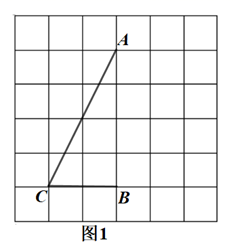
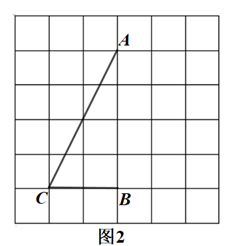 (1)、在图1中画出∠APB,使得∠APB=∠ACB,点P为格点.(2)、在图2中画出∠AMB,使得∠AMB+∠ACB=180°,点M为格点.21. 如图,二次函数y=x2+bx+c的图象与x轴分别交于点A,B(3,0)(点A在点B的左侧),与y轴交于点C,且经过点(﹣2,5).
(1)、在图1中画出∠APB,使得∠APB=∠ACB,点P为格点.(2)、在图2中画出∠AMB,使得∠AMB+∠ACB=180°,点M为格点.21. 如图,二次函数y=x2+bx+c的图象与x轴分别交于点A,B(3,0)(点A在点B的左侧),与y轴交于点C,且经过点(﹣2,5).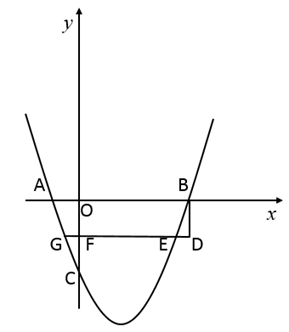 (1)、求b,c的值.(2)、将点B向下平移m个单位至点D,过点D作DF⊥y轴于点F,交抛物线于点E,G.若DE=GF,求m的值.22. 如图,在Rt△ACB中,∠ACB=90°,点D为BC延长线上一点,以BD为直径作半圆O分别交AB,AC于点G,E,点E为 的中点,过点E作⊙O的切线交AB于点F.
(1)、求b,c的值.(2)、将点B向下平移m个单位至点D,过点D作DF⊥y轴于点F,交抛物线于点E,G.若DE=GF,求m的值.22. 如图,在Rt△ACB中,∠ACB=90°,点D为BC延长线上一点,以BD为直径作半圆O分别交AB,AC于点G,E,点E为 的中点,过点E作⊙O的切线交AB于点F.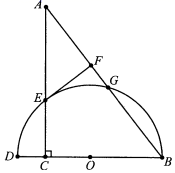 (1)、求证:∠AEF=∠ABC.(2)、若sinA= ,FG=1,求AC的长.23. 某经销商以每箱12元的价格购进一批消毒水进行销售,当每箱售价为26元时,日均销量为60箱.为了增加销量,该经销商准备适当降价.经市场调查发现,每箱消毒水降价1元,则可以多销售5箱,设每箱降价x元,日均销量为y箱.(1)、求日均销量y关于x的函数关系式.(2)、要使日均利润为800元,则每箱应降价多少元?(3)、促销后发现,该经销商每天的销售量不低于85箱.若每销售一箱消毒水可以享受政府m元(0<m≤6)的补贴,且销售这种消毒水的日均最大利润为1020元,求m的值.24. 如图1,在矩形ABCD中,AD=4,点O为BC的中点,将△DCO沿DO翻折至△DGO,直线DG分别交直线BC,直线AB于点E,F,连接BG.
(1)、求证:∠AEF=∠ABC.(2)、若sinA= ,FG=1,求AC的长.23. 某经销商以每箱12元的价格购进一批消毒水进行销售,当每箱售价为26元时,日均销量为60箱.为了增加销量,该经销商准备适当降价.经市场调查发现,每箱消毒水降价1元,则可以多销售5箱,设每箱降价x元,日均销量为y箱.(1)、求日均销量y关于x的函数关系式.(2)、要使日均利润为800元,则每箱应降价多少元?(3)、促销后发现,该经销商每天的销售量不低于85箱.若每销售一箱消毒水可以享受政府m元(0<m≤6)的补贴,且销售这种消毒水的日均最大利润为1020元,求m的值.24. 如图1,在矩形ABCD中,AD=4,点O为BC的中点,将△DCO沿DO翻折至△DGO,直线DG分别交直线BC,直线AB于点E,F,连接BG.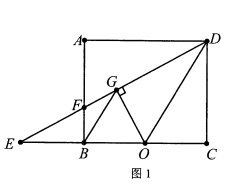 (1)、试判断BG与OD的位置关系,并说明理由.(2)、如图2,连接AC分别交DE,OD于点H,若AC⊥DE,
(1)、试判断BG与OD的位置关系,并说明理由.(2)、如图2,连接AC分别交DE,OD于点H,若AC⊥DE,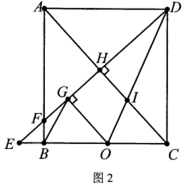
①求证:OB=2BE.
②求DI的长.
(3)、设直线BG交AD于点K,连接OK,记△ODK的面积为S1 , △BOG的面积为S2 , 连接OF,当△DOF中有一个内角的正切值为 时,求 的值.