新疆阿勒泰地区2021年数学中考模拟试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. 下列各数是正数的是( )A、 B、 C、 D、2. 在下图的四个立体图形中,从正面看是四边形的立体图形有( )
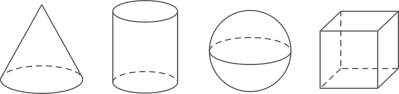 A、1个 B、2个 C、3个 D、4个3. 下列计算中正确的是( )A、 B、 C、 D、4. 如图, 为一长条形纸带, ,将 沿 折叠, 两点分别与 对应,若 ,则 的度数是( )
A、1个 B、2个 C、3个 D、4个3. 下列计算中正确的是( )A、 B、 C、 D、4. 如图, 为一长条形纸带, ,将 沿 折叠, 两点分别与 对应,若 ,则 的度数是( ) A、 B、 C、 D、5. 某班17名女同学的跳远成绩如下表所示:
A、 B、 C、 D、5. 某班17名女同学的跳远成绩如下表所示:成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
这些女同学跳远成绩的众数和中位数分别是( )
A、1.70,1.75 B、1.75,1.70 C、1.70,1.70 D、1.75,1.7256. 已知关于x的一元二次方程(m﹣1)x2﹣2x+1=0有实数根,则m的取值范围是( )A、m≤2 B、m≥2 C、m≤2且m≠1 D、m≥﹣2且m≠17. 某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( ).A、 B、 C、 D、8. 如图,在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于 AB长为半径作弧,两弧相交于M,N两点;②作直线MN交BC于点D,连接AD.若AD=AC,∠B=25°,则∠C=( ) A、70° B、60° C、50° D、40°9. 如图所示, 、 分别是正方形 的边 、 上的点,且 , , ,现有如下结论:① ;② ;③ ;④ .其中,正确的结论有( )
A、70° B、60° C、50° D、40°9. 如图所示, 、 分别是正方形 的边 、 上的点,且 , , ,现有如下结论:① ;② ;③ ;④ .其中,正确的结论有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
10. 在函数 中,自变量 的取值范围是.11. 将数12000000科学记数法表示为 .12. 一个多边形的每一个外角都等于45°,则这个多边形的内角和为13. 在某一时刻,测得一根高为 的竹竿的影长为 ,同时同地测得一栋楼的影长为 ,则这栋楼的高度为 .14. 如图,直线y= x与双曲线y= (k>0,x>0)交于点A,将直线y= x向上平移2个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=3BC,则k的值为.
 15. 如图所示,二次函数 ( , , , 为实数)的图象过点 ,对称轴为直线 ,给出以下结论:① ;② ;③ ;④若 、 为函数图象上的两点,则 .其中正确的有.(填写序号即可)
15. 如图所示,二次函数 ( , , , 为实数)的图象过点 ,对称轴为直线 ,给出以下结论:① ;② ;③ ;④若 、 为函数图象上的两点,则 .其中正确的有.(填写序号即可)
三、解答题
-
16. 计算 .17. 先化简,再求值 ,其中 满足
18. 如图所示,菱形 的对角线 、 相交于点 ,过点 作 ,且 ,连接 、 ,连接 交 于点 .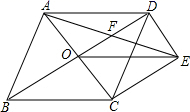 (1)、求证: ;(2)、若菱形 的边长为8, ,求 的长19. 如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据: , , 结果精确到0.1小时)
(1)、求证: ;(2)、若菱形 的边长为8, ,求 的长19. 如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据: , , 结果精确到0.1小时) 20. 某中学为了提高学生的综合素质,成立了以下社团: .机器人, .围棋, .羽毛球, .电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图,其中图(1)中 所占扇形的圆心角为 .
20. 某中学为了提高学生的综合素质,成立了以下社团: .机器人, .围棋, .羽毛球, .电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图,其中图(1)中 所占扇形的圆心角为 .
根据以上信息,解答下列问题:
(1)、这次被调查的学生共有人;(2)、请你将条形统计图补充完整;(3)、若该校共有 学生加入了社团,请你估计这 名学生中有多少人参加了羽毛球社团;(4)、在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.21. 如图,OA、BC分别是普通列车和动车从甲地开往乙地的路程 与时间 的函数图象,请根据图中的信息,解答下列问题: (1)、根据图象信息,普通列车比动车早出发h,动车的平均速度是 ;(2)、分别求出OA、BC的函数表达式,并写出自变量x的取值范围;(3)、动车出发多少小时追上普通列车?此时他们距离出发地多少千米?22. 如图, 是⊙ 的直径,弦 ,垂足为 ,连接 .过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 .
(1)、根据图象信息,普通列车比动车早出发h,动车的平均速度是 ;(2)、分别求出OA、BC的函数表达式,并写出自变量x的取值范围;(3)、动车出发多少小时追上普通列车?此时他们距离出发地多少千米?22. 如图, 是⊙ 的直径,弦 ,垂足为 ,连接 .过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 .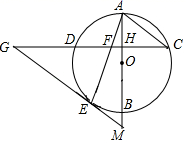 (1)、求证: 是⊙ 的切线;(2)、延长 交 的延长线于点 ,若 , ,求 的长.23. 已知,如图,抛物线 的顶点为 ,经过抛物线上的两点 和 的直线交抛物线的对称轴于点 .
(1)、求证: 是⊙ 的切线;(2)、延长 交 的延长线于点 ,若 , ,求 的长.23. 已知,如图,抛物线 的顶点为 ,经过抛物线上的两点 和 的直线交抛物线的对称轴于点 . (1)、求抛物线的解析式和直线 的解析式.(2)、在抛物线上 两点之间的部分(不包含 两点),是否存在点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由.(3)、若点 在抛物线上,点 在 轴上,当以点 为顶点的四边形是平行四边形时,直接写出满足条件的点 的坐标.
(1)、求抛物线的解析式和直线 的解析式.(2)、在抛物线上 两点之间的部分(不包含 两点),是否存在点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由.(3)、若点 在抛物线上,点 在 轴上,当以点 为顶点的四边形是平行四边形时,直接写出满足条件的点 的坐标.