四川省自贡市2021年数学中考适应性试卷

试卷更新日期：2021-05-08 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2$ 的相反数是（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 自贡市总人口超过300万，数300万用科学记数法可以表示为（）

A、 $3 \times 10^{2}$ B、 $3 \times 10^{3}$ C、 $3 \times 10^{6}$ D、 $300 \times 10^{4}$

查看试题解析
3. 计算 ${(- 1)}^{3} - \sqrt{16} + {(- 2)}^{0}$ 的结果是（）

A、－2 B、－4 C、－6 D、－7

查看试题解析
4. 如图，将一块含有30°的直角三角板的顶点放在直尺的一边上，若 $∠ 2 = 110 °$ ，那么 $∠ 1$ 的度数是（）

A、10° B、20° C、30° D、40°

查看试题解析
5. 某小区14户家庭的日用电量（单位：千瓦时）统计如下：

日用电量（单位：千瓦时）

3

4

5

6

7

8

户数

1

6

3

2

1

1

这14户家庭日用电量的众数、中位数分别是（）

A、4，4.5 B、4，5.5 C、6，1.5 D、1，1.5

查看试题解析
6. 若正多边形的内角和是720°，则该正多边形的一个外角为（）

A、20° B、30° C、45 D、60°

查看试题解析
7. 三张质地、大小、背面完全相同的卡片上，正面分别画有圆、矩形、等边三角形三个图案.现把它们的正面向下随机摆放在桌面上，从中任意抽出两张，则抽出的卡片正面图案都是中心对称图形的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、 $\frac{2}{3}$

查看试题解析
8. 如图，在平行四边形 $A B C D$ 中，F为BC中点，延长AD至E，连结EF交DC于点G，若 $S_{△ D G E} ： S_{△ C G F} = 4 ： 9$ ，则 $D E ： A D =$ （）

A、1：2 B、1：3 C、1：4 D、2：9

查看试题解析
9. 2021年自贡环青龙湖半程马拉松的赛程是21.0975公里，甲乙两选手的行程y（千米）随时间x（时）变化的图象（全程）如图所示.有下列说法：①第1小时两人都跑了10千米；②起跑1小时过后，甲在乙的后面；③在起跑后的0.5至1.5小时，甲比乙跑得更慢；④乙比甲先到达终点其中正确的说法有（）

A、 1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，BC为 $⊙ O$ 直径，若 $∠ A = 80 °$ ， $B C = 6$ ，则图中灰色区域的面积为（）

A、 $2 π$ B、 $3 π$ C、 $4 π$ D、 $5 π$

查看试题解析
11. 如图，在平面直角坐标系中，点O为坐标原点，平行四边形 $O A B C$ 的顶点A在反比例函数 $y = \frac{2}{x}$ 上，顶点B在反比例函数 $y = \frac{6}{x}$ 上，点C在x轴的正半轴上，则平行四边形 $O A B C$ 的面积是（）

A、2 B、3 C、4 D、5

查看试题解析
12. 如图，已知 $A B = 8$ ，P为线段AB上的一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE，点P，C，E在一条直线上， $∠ D A P = 60 °$ ，M，N分别是对角线AC，BE的中点.当点Р在线段AB上移动时，点MN之间的距离最短为（）

A、2 B、 $2 \sqrt{3}$ C、4 D、 $4 \sqrt{3}$

查看试题解析

二、填空题

13. $| - \sqrt{3} |$ =

查看试题解析
14. 如图，在正方形ABCD的外侧，作等边 $△ A D E$ ，连接BE、CE， $∠ C B E$ 的度数是.

查看试题解析
15. $\sqrt[3]{7}$ ， $- π$ ，2，0这四个数中，最大的数是.

查看试题解析
16. 如图，AB是 $⊙ O$ 的切线，半径 $O A = 3$ ，OB交 $⊙ O$ 于 $C$ ， $∠ A O B = 60 °$ ，则BC的长是.

查看试题解析
17. 某工厂生产一批零件，计划20天完成，若每天多生产5个，则16天完成且还多生产8个.设原计划每天生产x个，根据题意可列方程为.

查看试题解析
18. 如图，反比例函数 $y = \frac{24}{x}$ （x＞0）的图象与直线 $y = \frac{3}{2} x$ 相交于点A，与直线y=kx（k≠0）相交于点B，若△OAB的面积为18，则k的值为.

查看试题解析

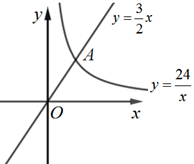
三、解答题

19. 先化简，再求值 $(\frac{m^{2} - 1}{m^{2} - 2 m + 1} - \frac{1}{1 - m}) \div \frac{2}{m^{2} - m}$ ，其中 $m$ 满足 $m^{2} + 2 m - 6 = 0$ .

查看试题解析
20. 如图，E、F分别为正方形ABCD的边DC、BC中点.求证： $A E = A F$ .

查看试题解析
21. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点都在格点上，点A的坐标为 $(2 ， 4)$ ，请解答下列问题：

①画出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $C_{1}$ 的坐标；

②画出 $△ A_{1} B_{1} C_{1}$ 关于原点对称的 $△ A_{2} B_{2} C_{2}$ ，并写出点 $C_{2}$ 的坐标.﹐

查看试题解析

22. 在世界环境日（6月5日），学校组织了保护环境知识测试，现从中随机抽取部分学生的成绩作为样本，按“优秀”“良好”“合格”“不合格”四个等级进行统计，绘制了如下尚不完整的统计图表.

等级	频数	频率
优秀	30	a
良好	b	0.45
合格	24	0.20
不合格	12	0.10
合计	c	1

根据统计图表提供的信息，解答下列问题：

(1)、表中

a =

，

b =

，

c =

；

(2)、补全条形统计图；

(3)、若该校有800名学生参加了本次测试，估计测试成绩等级在良好以上（包括良好）的学生约有多少人？

查看试题解析

23. 如图，BC是 $⊙ O$ 的直径，CE是 $⊙ O$ 的弦，过点E作 $⊙ O$ 的切线，交 CB的延长线于点G，过点B作 $B F ⊥ G E$ 于点F，交CE的延长线于点A.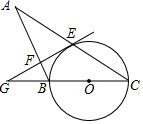

(1)、求证： $A B = B C$ ；

(2)、若 $G F = 2 \sqrt{3}$ ， $B F = 2$ ，求 $⊙ O$ 的半径.

查看试题解析
24. 对于三个实数a，b，c，用 $M {a, b, c}$ 表示这三个数的平均数，用min ${a, b, c}$ 表示这三个数中最小的数.例如： $M {1, 2, 9} = \frac{1 + 2 + 9}{3} = 4$ ，min ${1, 2, - 3} = - 3$ ，min ${3, 1, 1} = 1$ .
请结合上述材料，解决下列问题：

(1)、 $M {3^{2}, {(- 3)}^{2}, - 3^{2}} =$ ；

(2)、若min ${2 x + 1, 4 x - 3, 7} = 2 x + 1$ ，则整数 $x$ 的值是；

(3)、若 $M {5 x, x^{2}, - 3} =$ min ${x^{2}, - 3}$ ，求 $x$ 的值.

查看试题解析
25. 已知抛物线 $y = a x^{2} + b x + 3$ 经过点 $A (1 ， 0)$ 和点 $B (- 3 ， 0)$ ，与y轴交于点C，点P为第二象限内抛物线上的动点.

(1)、抛物线的解析式为，抛物线的顶点坐标为；

(2)、如图1，是否存在点P，使四边形BOCP的面积为9？若存在，请求出点P的坐标；若不存在，请说明理由；

(3)、如图2，当 $△ B P C$ 的面积最大时，连接OP交BC于点D，请求出点D的坐标.

查看试题解析
26. 如图①，在钝角 $△ A B C$ 中， $∠ A B C = 30 °$ ， $A C = 10$ ，点D为边AB的中点，点E为边BC的中点，将 $△ B D E$ 绕点B逆时针方向旋转 $α$ 度 $(0 \leq a \leq 180 °)$ .

(1)、如图②，当 $0 < α < 180 °$ 时，连接AD、CE.求证： $△ B D A ∽ △ B E C$ ；

(2)、如图③，直线CE、AD交于点G.在旋转过程中， $∠ A G C$ 的大小是否发生变化？如变化，请说明理由；如不变，请求出这个角的度数；

(3)、将 $△ B D E$ 从图①位置绕点B逆时针方向旋转180°，求点G的运动路程.

查看试题解析

日用电量（单位：千瓦时）	3	4	5	6	7	8
户数	1	6	3	2	1	1