辽宁省铁岭市部分校2021年数学中考模拟试卷(一)
试卷更新日期:2021-05-06 类型:中考模拟
一、单选题
-
1. —2021的绝对值是( )A、2021 B、 C、 D、2. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、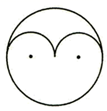 D、
D、 3. 下面几何体的俯视图是( )
3. 下面几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 关于一组数据: ,1,1,2,下列说法中不正确的是( )A、平均数是0.5 B、众数是1 C、中位数是1 D、方差是0.756. 如图,点 , , 在 上, ,过点 作 的切线交 的延长线于点 ,则 的大小为( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 关于一组数据: ,1,1,2,下列说法中不正确的是( )A、平均数是0.5 B、众数是1 C、中位数是1 D、方差是0.756. 如图,点 , , 在 上, ,过点 作 的切线交 的延长线于点 ,则 的大小为( ) A、26° B、38° C、48° D、52°7. 在一个不透明的袋子中装有2个红球和3个黑球,它们除颜色外其他均相同,从中任意摸出1个球,则摸出黑球的概率是( )A、 B、 C、 D、8. 如图,在 中, 为边 的中点, 于点 , , , ,则 ( )
A、26° B、38° C、48° D、52°7. 在一个不透明的袋子中装有2个红球和3个黑球,它们除颜色外其他均相同,从中任意摸出1个球,则摸出黑球的概率是( )A、 B、 C、 D、8. 如图,在 中, 为边 的中点, 于点 , , , ,则 ( ) A、60° B、75° C、90° D、105°9. 如图,在矩形 中,点 , 分别在边 和 上,把该矩形沿 折叠,使点 恰好落在边 的点 处,已知矩形 的面积为 , ,则折痕 的长为( )
A、60° B、75° C、90° D、105°9. 如图,在矩形 中,点 , 分别在边 和 上,把该矩形沿 折叠,使点 恰好落在边 的点 处,已知矩形 的面积为 , ,则折痕 的长为( )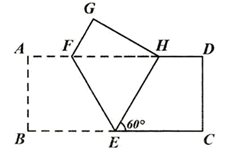 A、 B、2 C、 D、410. 数学课上老师出了这样一道题:如图,抛物线 的对称轴为直线 ,与 轴的一个交点在 和 之间,其部分图像如图所示,请同学们据此写出正确结论,每写对一个结论得20分,写错一个结论倒扣10分;
A、 B、2 C、 D、410. 数学课上老师出了这样一道题:如图,抛物线 的对称轴为直线 ,与 轴的一个交点在 和 之间,其部分图像如图所示,请同学们据此写出正确结论,每写对一个结论得20分,写错一个结论倒扣10分;
小涛得到了如下结论:① ;② ;③ ;④ ( 为实数);⑤点 , , 是该抛物线的点,则 .则小涛此题得分为( )
A、100分 B、70分 C、40分 D、10分二、填空题
-
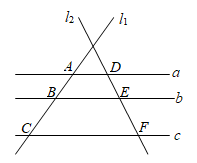
11. 据猫眼专业版实时数据显示,电影《你好,李焕英》总票房达到5012000000元,在中国影史票房排行仅次于《战狼2》和《哪吒之魔童降世》,目前排行第三,将数据5012000000用科学记数法可以表示为 .12. 分解因式: .13. 如图, ,直线 , 与这三条平行线分别交于点 , , 和点 , , .若 , , ,则 .
 14. 如图,点 为 内部一点,连接 , ,量得 ,图中的三个扇形(阴影部分)的半径均为1,则阴影部分的总面积为 .
14. 如图,点 为 内部一点,连接 , ,量得 ,图中的三个扇形(阴影部分)的半径均为1,则阴影部分的总面积为 . 15. 在 中, , , ,则 的面积是 .16. 如图所示是一块含30°角的直角三角板,直角顶点 位于坐标原点,斜边 轴,顶点 在函数 的图像上,顶点 在 的图像上, ,则
15. 在 中, , , ,则 的面积是 .16. 如图所示是一块含30°角的直角三角板,直角顶点 位于坐标原点,斜边 轴,顶点 在函数 的图像上,顶点 在 的图像上, ,则 17. 如图,点 为正方形 的边 的延长线上一点,以 为边在 的另一侧作正方形 ,连接 ,若 , ,则 的面积为 .
17. 如图,点 为正方形 的边 的延长线上一点,以 为边在 的另一侧作正方形 ,连接 ,若 , ,则 的面积为 . 18. 如图,在平面直角坐标系中,直线 交 轴于点 ,交 轴于点 ,点 , ,…在直线1上,点 ,点 , ,…在 轴的正半轴上,若 , , ,…均为等腰直角三角形,直角顶点都在 轴上,则第 个等腰直角三角形 的顶点 的坐标为 .
18. 如图,在平面直角坐标系中,直线 交 轴于点 ,交 轴于点 ,点 , ,…在直线1上,点 ,点 , ,…在 轴的正半轴上,若 , , ,…均为等腰直角三角形,直角顶点都在 轴上,则第 个等腰直角三角形 的顶点 的坐标为 .
三、解答题
-
19. 先化简,再求值: ,其中20. 随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五•一”长假期间旅游情况统计图,根据以下信息解答下列问题:
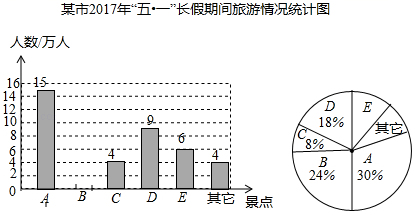 (1)、2017年“五·一”期间,该市周边景点共接待游客多少万人,扇形统计图中A景点所对应的圆心角的度数是多少,并补全条形统计图.(2)、根据近几年到该市旅游人数增长趋势,预计2018年“五•一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?(3)、甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.21. 鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售量为y个.(1)、直接写出销售量y个与降价x元之间的函数关系式;(2)、设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?22. 如图,反比例函数 的图像与一次函数 的图像在第一象限内相交于点 .
(1)、2017年“五·一”期间,该市周边景点共接待游客多少万人,扇形统计图中A景点所对应的圆心角的度数是多少,并补全条形统计图.(2)、根据近几年到该市旅游人数增长趋势,预计2018年“五•一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?(3)、甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.21. 鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售量为y个.(1)、直接写出销售量y个与降价x元之间的函数关系式;(2)、设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?22. 如图,反比例函数 的图像与一次函数 的图像在第一象限内相交于点 .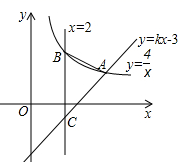 (1)、求 的值及一次函数的解析式;(2)、直线 与反比例函数和一次函数的图象分别交于点 , ,求 的面积.23. 如图, 是 的直径, ,点 是劣弧 上一点,过点 作 的切线 ,交 的延长线于点 , 交 于点 .
(1)、求 的值及一次函数的解析式;(2)、直线 与反比例函数和一次函数的图象分别交于点 , ,求 的面积.23. 如图, 是 的直径, ,点 是劣弧 上一点,过点 作 的切线 ,交 的延长线于点 , 交 于点 . (1)、求证: ;(2)、若 , ,过点 作 交 于点 ,求 的长.24. 如图, 地在 地的正西方向,因有大山阻隔,由 地到 地需绕行 地,已知 地位于 地北偏西67°方向,距离 地117千米, 地位于 地南偏西30°方向,若打通穿山隧道,建成两地直达高铁,求 地到 地之间高铁线路的长.
(1)、求证: ;(2)、若 , ,过点 作 交 于点 ,求 的长.24. 如图, 地在 地的正西方向,因有大山阻隔,由 地到 地需绕行 地,已知 地位于 地北偏西67°方向,距离 地117千米, 地位于 地南偏西30°方向,若打通穿山隧道,建成两地直达高铁,求 地到 地之间高铁线路的长.(结果保留整数,参考数据: , , , )
 25. 如图,半径为7的 上有一动点 ,点 为半径 上一点,且 最大为10,以 为边向外作正方形 ,连接 .
25. 如图,半径为7的 上有一动点 ,点 为半径 上一点,且 最大为10,以 为边向外作正方形 ,连接 .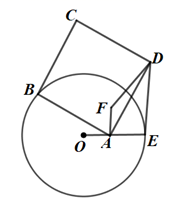 (1)、请直接写出 的长;(2)、过点 作 ,且 ,连接 ,在点 的运动过程中, 的长度会发生变化吗?变化请说明理由,不变化请求出 的长;(3)、当点A,B,F三点在一条直线上时,请直接写 的长;(4)、请直接写出 的最大值和最小值.26. 如图,已知二次函数 的图象分别交 轴于点 , ,交 轴于点 ,抛物线的顶点为 ,其中点 , , .
(1)、请直接写出 的长;(2)、过点 作 ,且 ,连接 ,在点 的运动过程中, 的长度会发生变化吗?变化请说明理由,不变化请求出 的长;(3)、当点A,B,F三点在一条直线上时,请直接写 的长;(4)、请直接写出 的最大值和最小值.26. 如图,已知二次函数 的图象分别交 轴于点 , ,交 轴于点 ,抛物线的顶点为 ,其中点 , , .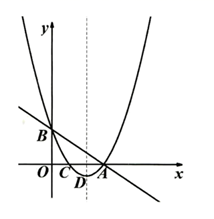 (1)、求抛物线的解析式并直接写出抛物线的对称轴;(2)、在直线 的上方抛物线上有一点 ,且满足 ,请求出点 的坐标;(3)、点 为对称轴上一点,点 为抛物线上一点,是否存在点 , ,使以点A,B,M,N为顶点的四边形是平行四边形?若存在请直接写出点 的坐标,若不存在请说明理由.
(1)、求抛物线的解析式并直接写出抛物线的对称轴;(2)、在直线 的上方抛物线上有一点 ,且满足 ,请求出点 的坐标;(3)、点 为对称轴上一点,点 为抛物线上一点,是否存在点 , ,使以点A,B,M,N为顶点的四边形是平行四边形?若存在请直接写出点 的坐标,若不存在请说明理由.