江苏省盐城市2021年数学中考模拟试卷
试卷更新日期:2021-05-06 类型:中考模拟
一、单选题
-
1. |﹣π|的相反数是( )A、﹣ B、 C、﹣ D、2. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、2a﹣a=2 B、a3·a2=a6 C、a3÷a=a2 D、(2a2)3=6a54. 实数a,b,c,d在数轴上对应点的位置如图所示,正确的结论是( )
3. 下列运算正确的是( )A、2a﹣a=2 B、a3·a2=a6 C、a3÷a=a2 D、(2a2)3=6a54. 实数a,b,c,d在数轴上对应点的位置如图所示,正确的结论是( )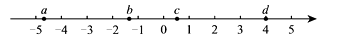 A、a > c B、b +c > 0 C、|a|<|d| D、-b<d5. 如图所示的几何体是由7个大小相同的小立方块搭成,其左视图是( )
A、a > c B、b +c > 0 C、|a|<|d| D、-b<d5. 如图所示的几何体是由7个大小相同的小立方块搭成,其左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 下列把2034000记成科学记数法正确的是( )A、2.034×106 B、20.34×105 C、0.2034×106 D、2.034×1037. 小涵在2020年某月的月历上圈出了三个数a,b,c,并求出了它们的和为30,则这三个数在月历中的排位位置不可能是( )A、
6. 下列把2034000记成科学记数法正确的是( )A、2.034×106 B、20.34×105 C、0.2034×106 D、2.034×1037. 小涵在2020年某月的月历上圈出了三个数a,b,c,并求出了它们的和为30,则这三个数在月历中的排位位置不可能是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,在菱形ABCD中,AC与BD相交于点O,点P是AB的中点,PO=2,则菱形ABCD的周长是( )
8. 如图,在菱形ABCD中,AC与BD相交于点O,点P是AB的中点,PO=2,则菱形ABCD的周长是( )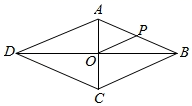 A、4 B、8 C、16 D、24
A、4 B、8 C、16 D、24二、填空题
-
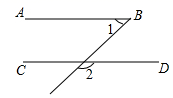
9. 如图,已知 ,则 的度数是.
 10. 一组数据3,2,1,4, 的平均数为3,则 的值是 .11. 因式分解: .12. 方程 = +3的解是.13. 在一个不透明的盒子里有形状、大小完全相同的黄球n个、红球3个,白球4个,从盒子里任意摸出一个球,摸到红球的概率是 ,则盒子里一共有个球.14. 如图,△ABC中,∠A=50°,以AB为直径的⊙O分别与BC,AC交于点D,E,且BD=CD,连接BE,DE,则∠BED的大小为.
10. 一组数据3,2,1,4, 的平均数为3,则 的值是 .11. 因式分解: .12. 方程 = +3的解是.13. 在一个不透明的盒子里有形状、大小完全相同的黄球n个、红球3个,白球4个,从盒子里任意摸出一个球,摸到红球的概率是 ,则盒子里一共有个球.14. 如图,△ABC中,∠A=50°,以AB为直径的⊙O分别与BC,AC交于点D,E,且BD=CD,连接BE,DE,则∠BED的大小为. 15. 如图,AB⊥BC,DC⊥BC,点E在BC上,AE⊥DE,DC=1,BE=3,BC=5,则AB=.
15. 如图,AB⊥BC,DC⊥BC,点E在BC上,AE⊥DE,DC=1,BE=3,BC=5,则AB=. 16. 如图,菱形 顶点 在函数 的图象上,函数 的图象关于直线 对称,且经过点 , 两点,若 , ,则 的值为.
16. 如图,菱形 顶点 在函数 的图象上,函数 的图象关于直线 对称,且经过点 , 两点,若 , ,则 的值为.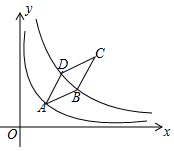
三、解答题
-
17. 计算: .18. 解不等式组: .19. 先化简:( )÷ ,再从﹣3、﹣2、﹣1、0、1中选一个合适的数作为a的值代入求值.20. 如图,在Rt△ABC中,∠BAC=90º,sinC= ,AC=8,BD平分∠ABC交边AC于点D.
 (1)、求边AB的长;(2)、求tan∠ABD的值.21. 如图,在△ABC中,∠A>∠B.
(1)、求边AB的长;(2)、求tan∠ABD的值.21. 如图,在△ABC中,∠A>∠B.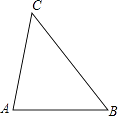 (1)、作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连接AE,若∠B=50°,求∠AEC的度数.22. 绿色出行是对环境影响最小的出行方式,“共享单车”已成为长春市的一道亮丽的风景线.某社会实践活动小组为了了解“共享单车”的使用情况,对本校师生在7月6日至7月10日使用单车的情况进行了问卷调查. 以下是根据调查结果绘制的统计图的一部分:
(1)、作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连接AE,若∠B=50°,求∠AEC的度数.22. 绿色出行是对环境影响最小的出行方式,“共享单车”已成为长春市的一道亮丽的风景线.某社会实践活动小组为了了解“共享单车”的使用情况,对本校师生在7月6日至7月10日使用单车的情况进行了问卷调查. 以下是根据调查结果绘制的统计图的一部分:

请根据以上信息解答下列问题:
(1)、7月7日使用“共享单车”的师生有人.(2)、不同品牌的“共享单车”各具特色,社会实践活动小组针对有过使用“共享单车”经历的师生做了进一步调查,每个人都按要求选择了一种自己喜欢的“共享单车”,统计结果如图,其中喜欢mobike的师生有36人.求喜欢ofo的师生人数.23. 中国籍作家莫言获2012年诺贝尔文学奖后,国内掀起了一股莫言作品的热潮.小明的语文老师是莫言的忠实读者,家中现有: .《透明的红萝卜》, .《红高粱家族》, .《生死疲劳》, .《蛙》等四部作品.(1)、若老师随机拿来一本给小明阅读,拿到《蛙》的概率是多少?(2)、若小明想向老师同时借阅两本,请用树形图或列表法的一种,列举出老师随机抽取两本时所有可能的结果(用 、 、 、 表示相应的作品),并求出小明恰好到《生死疲劳》和《蛙》的概率.24. 如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.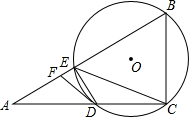 (1)、求证:DF是⊙O的切线.(2)、若D是AC的中点,∠A=30°,BC=4,求DF的长.25. 若二次函数 的图象与 轴有两个交点 ,且经过点 过点 的直线 与 轴交于点 与该函数的图象交于点 (异于点 ).满足 是等腰直角三角形,记 的面积为 的面积为 ,且 .
(1)、求证:DF是⊙O的切线.(2)、若D是AC的中点,∠A=30°,BC=4,求DF的长.25. 若二次函数 的图象与 轴有两个交点 ,且经过点 过点 的直线 与 轴交于点 与该函数的图象交于点 (异于点 ).满足 是等腰直角三角形,记 的面积为 的面积为 ,且 . (1)、抛物线的开口方向(填“上”或“下”);(2)、求直线 相应的函数表达式;(3)、求该二次函数的表达式.26. 如图,在Rt△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D,AD=4cm,过点D作DE∥AC,交AB于点E,DF∥AB,交AC于点F.动点P从点A出发以1cm/s的速度向终点D运动,过点P作MN∥BC,交AB于点M,交AC于点N.设点P运动时间为x (s),△AMN与四边形AEDF重叠部分面积为y(cm2).
(1)、抛物线的开口方向(填“上”或“下”);(2)、求直线 相应的函数表达式;(3)、求该二次函数的表达式.26. 如图,在Rt△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D,AD=4cm,过点D作DE∥AC,交AB于点E,DF∥AB,交AC于点F.动点P从点A出发以1cm/s的速度向终点D运动,过点P作MN∥BC,交AB于点M,交AC于点N.设点P运动时间为x (s),△AMN与四边形AEDF重叠部分面积为y(cm2). (1)、AE=cm,AF=cm;(2)、求y关于x的函数解析式,并写出x的取值范围;(3)、若线段MN中点为O,当点O落在∠ACB平分线上时,直接写出x的值.27. 如图,抛物线 交 轴于 、 两点,其中点 坐标为 ,与 轴交于点 .
(1)、AE=cm,AF=cm;(2)、求y关于x的函数解析式,并写出x的取值范围;(3)、若线段MN中点为O,当点O落在∠ACB平分线上时,直接写出x的值.27. 如图,抛物线 交 轴于 、 两点,其中点 坐标为 ,与 轴交于点 .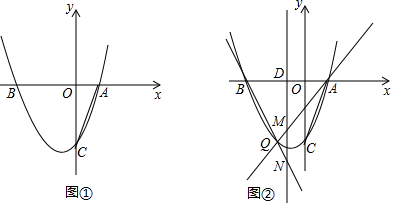 (1)、求抛物线的函数表达式;(2)、如图①,连接 ,点 在抛物线上,且满足 .求点 的坐标;(3)、如图②,点 为 轴下方抛物线上任意一点,点 是抛物线对称轴与 轴的交点,直线 、 分别交抛物线的对称轴于点 、 .请问 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
(1)、求抛物线的函数表达式;(2)、如图①,连接 ,点 在抛物线上,且满足 .求点 的坐标;(3)、如图②,点 为 轴下方抛物线上任意一点,点 是抛物线对称轴与 轴的交点,直线 、 分别交抛物线的对称轴于点 、 .请问 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.