江苏省无锡市2021年数学中考模拟试卷
试卷更新日期:2021-05-06 类型:中考模拟
一、单选题
-
1. 若a、b互为倒数,则2ab-5的值为( )A、1 B、2 C、-3 D、-52. 函数y= 中自变量x的取值范围是( )A、x≥3且x≠5 B、x>3且x≠5 C、x<3且x≠5 D、x≤3且x≠53. 如表所示是某位运动员近6次的比赛成绩(单位:分钟):
第几次
1
2
3
4
5
6
比赛成绩
40
50
35
20
25
10
则这组成绩的中位数和平均数分别为( )
A、25.25 ,30 B、30 ,85 C、27.5 ,85 D、30 , 304. 下列计算正确的是( )A、 B、 C、 D、5. 一个正多边形,它的一个内角恰好是一个外角的 倍,则这个正多边形的边数是( )A、八 B、九 C、十 D、十二6. 下列四个图案中,是中心对称图形,但不是轴对称图形的是( )A、 B、
B、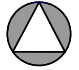 C、
C、 D、
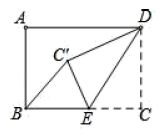
D、 7. 下列运算正确的是( )A、 B、 C、 D、8. 已知反比例函数 与一次函数叫 的图象没有交点,则k的值可以是( )A、 B、 C、 D、9. 如图,在四边形ABCD中,∠ABC=∠BCD=90°, ,把 沿着AC翻折得到 ,若 ,则线段DE的长度( )
7. 下列运算正确的是( )A、 B、 C、 D、8. 已知反比例函数 与一次函数叫 的图象没有交点,则k的值可以是( )A、 B、 C、 D、9. 如图,在四边形ABCD中,∠ABC=∠BCD=90°, ,把 沿着AC翻折得到 ,若 ,则线段DE的长度( ) A、 B、 C、 D、10. 如图,正三角形ABC的边长为3+ ,在三角形中放入正方形DEMN和正方形EFPH,使得D,E,F在边AB上,点P、N分别在边CB、CA上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
A、 B、 C、 D、10. 如图,正三角形ABC的边长为3+ ,在三角形中放入正方形DEMN和正方形EFPH,使得D,E,F在边AB上,点P、N分别在边CB、CA上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )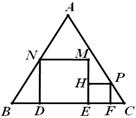 A、 B、 C、3 D、
A、 B、 C、3 D、二、填空题
-
11. 因式分解: .12. 2020年6且23日,北斗三号最后一颗全球组网卫星从西昌发射中心发射升空,6月30日成功定点于距离地球36000公里的地球同步轨道.将36000用科学记数法表示应为.13. 如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是 元(结果保留整数).
 14. 如图,在边长为10的菱形ABCD中,对角线BD=16,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则OE+OF=.
14. 如图,在边长为10的菱形ABCD中,对角线BD=16,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则OE+OF=.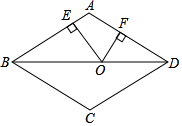 15. 写出一个二次函数关系式,使其图象开口向上.16. 一天,小民去问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,125岁了,哈哈!”请你写出小民爷爷到底是岁.17. 已知函数y=kx2+(2k+1)x+1(k为实数).
15. 写出一个二次函数关系式,使其图象开口向上.16. 一天,小民去问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,125岁了,哈哈!”请你写出小民爷爷到底是岁.17. 已知函数y=kx2+(2k+1)x+1(k为实数).( 1 )对于任意实数k,函数图象一定经过点(﹣2,﹣1)和点;
( 2 )对于任意正实数k,当x>m时,y随着x的增大而增大,写出一个满足题意的m的值为.
18. 如图,直线l1∥l2∥l3 , 分别交直线m、n于点A、B、C、D、E、F,若AB:BC=5:3,DE=15,则EF的长为.
三、解答题
-
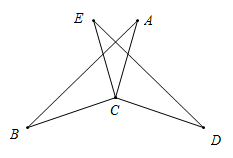
19. 计算:(1)、 .(2)、 .20. 解方程与不等式组(1)、解方程:(x+1)(x+3)=15(2)、解方程:3x2﹣2x=2(3)、解不等式组21. 如图,已知EC=AC,∠BCE=∠ACD,∠A=∠E,BC=3.求DC的值.
 22. 将分别标有数字1、2、3的3个质地和大小完全相同的小球装在一个不透明的口袋中.(1)、若从口袋中随机摸出一个球,其标号为奇数的概率为多少?(2)、若从口袋中随机摸出一个球,放回口袋中搅匀后再随机摸出一个球,试求所摸出的两个球上数字之和等于4的概率(用树状图或列表法求解).23. 莫拉克台风给台湾造成了重大的损失,某中学开展爱心捐助活动,根据预备年级的捐款情况绘制如下统计图:
22. 将分别标有数字1、2、3的3个质地和大小完全相同的小球装在一个不透明的口袋中.(1)、若从口袋中随机摸出一个球,其标号为奇数的概率为多少?(2)、若从口袋中随机摸出一个球,放回口袋中搅匀后再随机摸出一个球,试求所摸出的两个球上数字之和等于4的概率(用树状图或列表法求解).23. 莫拉克台风给台湾造成了重大的损失,某中学开展爱心捐助活动,根据预备年级的捐款情况绘制如下统计图: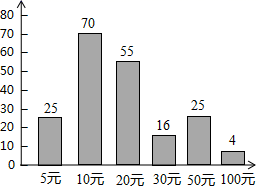
请根据统计图给出的信息回答下列问题:
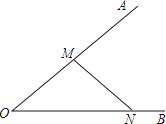
(1)、本次活动中预备年级共有多少同学捐款?(2)、本次活动中捐款20元以上(不包括捐款20元的)的人数占预备年级捐款总人数的几分之几?24.如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
 25. 如图:CB与圆O相切于B,半径OA⊥OC,AB、OC相交于D,求证:
25. 如图:CB与圆O相切于B,半径OA⊥OC,AB、OC相交于D,求证: (1)、CD=CB;(2)、AD·DB=2CD·DO.26. 某水果店销售某种水果,由市场行情可知,从1月至12月,这种水果每千克售价 (元)与销售时间 ( , 为正整数)月之间存在如图1所示(图1的图象是线段)的变化趋势,每千克成本 (元)与销售时间 ( , 为正整数)月满足函数表达式 ,其变化趋势如图2所示(图2的图象是抛物线).
(1)、CD=CB;(2)、AD·DB=2CD·DO.26. 某水果店销售某种水果,由市场行情可知,从1月至12月,这种水果每千克售价 (元)与销售时间 ( , 为正整数)月之间存在如图1所示(图1的图象是线段)的变化趋势,每千克成本 (元)与销售时间 ( , 为正整数)月满足函数表达式 ,其变化趋势如图2所示(图2的图象是抛物线).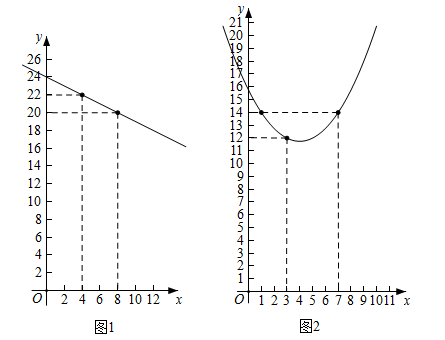 (1)、求 关于 的函数表达式(不需要写出自变量的取值范围)(2)、求 关于 的函数表达式(不需要写出自变量的取值范围)(3)、求哪个月出售这种水果,每千克所获得的收益最大.
(1)、求 关于 的函数表达式(不需要写出自变量的取值范围)(2)、求 关于 的函数表达式(不需要写出自变量的取值范围)(3)、求哪个月出售这种水果,每千克所获得的收益最大.