江苏省南京市2021年数学中考模拟试卷

试卷更新日期：2021-05-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 今年2月份某市一天的最高气温为10℃，最低气温为﹣7℃，那么这一天的最高气温比最低气温高（）

A、﹣17℃ B、17℃ C、5℃ D、11℃

查看试题解析
2. 9的平方根是( )

A、3　 B、±3　　 C、 $\sqrt{3}$ 　　 D、± $\sqrt{3}$

查看试题解析
3. 下列运算正确的是（）

A、m²·m³=m⁶ B、m⁸÷m⁴=m² C、3m+2n=5mn D、（m³）²=m⁶

查看试题解析
4. 2019年以来，中美经贸摩擦影响持续显现，我国对外贸易仍然表现出很强的韧性.进出口保持稳中提质的发展势头，如图是某省近五年进出口情况统计图，下列描述错误的是（）

A、这五年，2015年出口额最少 B、这五年，出口总额比进口总额多 C、这五年，出口增率前四年逐年下降 D、这五年，2019年进口增率最快

查看试题解析
5. 关于方程x²＋2x﹣4＝0的根的情况，下列结论错误的是（）

A、有两个不相等的实数根 B、两实数根的和为2 C、两实数根的差为 $\pm 2 \sqrt{5}$ D、两实数根的积为﹣4

查看试题解析
6. 如图，在矩形ABCD中，AB＝4，AD＝8，点E、点F分别在边AD，BC上，且EF⊥AD，点B关于EF的对称点为G点，连接EG，若EG与以CD为直径的⊙O恰好相切于点M，则AE的长度为（）

A、3 B、 $\sqrt{10}$ C、6+ $\sqrt{6}$ D、6﹣ $\sqrt{6}$

查看试题解析

二、填空题

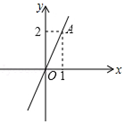
7. 写出一个负数，使这个数的绝对值小于4.

查看试题解析
8. 当x时，分式 $\frac{x + 2}{x - 3}$ 有意义.

查看试题解析
9. 将0.0012用科学记数法表示为.

查看试题解析
10. 计算 $\frac{21}{\sqrt{7}} - \sqrt{28}$ 的结果是.

查看试题解析
11. 已知m、n满足方程组 ${\begin{array}{l} m + 5 n = 7 \\ 3 m - n = 9 \end{array}$ ，则m＋n的值是.

查看试题解析
12. 方程 $\frac{1}{x + 3} = \frac{3}{x}$ 的解为.

查看试题解析
13. 如图，将直线OA向上平移2个单位长度，则平移后的直线的表达式为。

查看试题解析
14. 如图，过正六边形ABCDEF的顶点D作一条直线l⊥AD于点D，分别延长AB、AF交直线l于点M，N，则∠AMN＝；若正六边形ABCDEF的面积为6，则△AMN的面积为 .

查看试题解析
15. 在△ABC中，AB、AC的垂直平分线分别交BC于D、E，∠DAE＝20°，则∠BAC＝°.

查看试题解析

16. 已知y是x的二次函数，y与x的部分对应值如下表：该二次函数图象向左平移个单位，图象经过原点.

x	…	﹣1	0	1	2	…
y	…	0	3	4	3	…

查看试题解析

三、解答题

17. 某班“数学兴趣小组”对函数y=

\frac{x}{x - 1}

，的图象和性质进行了探究探究过程如下，请补充完成：

(1)、函数y=

\frac{x}{x - 1}

的自变量x的取值范围是；

(2)、下表是y与x的几组对应值.请直接写出m，n的值：m=；n= .

…

﹣2

﹣1

$\frac{1}{2}$

$\frac{3}{4}$

$\frac{5}{4}$

…

$\frac{2}{3}$

﹣1

﹣3

$\frac{3}{2}$

$\frac{4}{3}$

…

(3)、如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；

(4)、通过观察函数的图象，小明发现该函数图象与反比例函数y=

\frac{k}{x}

（k＞0）的图象形状相同，是中心对称图形，且点（﹣1，m）和（3，

\frac{3}{2}

）是一组对称点，则其对称中心的坐标为.

(5)、当2≤x≤4时，关于x的方程kx+

\frac{1}{2}

\frac{x}{x - 1}

有实数解，求k的取值范围.

查看试题解析

18. 计算： $\frac{1}{a - 1} + \frac{a - 3}{a^{2} + 2 a + 1} \div \frac{a - 1}{a + 1}$ .

查看试题解析
19. 解方程： $2 x^{2} - 3 x - 5 = 0$

查看试题解析
20. 如图，已知AB＝AE，∠B＝∠E，BC＝ED，AF⊥CD.求证：F是CD的中点.

查看试题解析
21. 一只不透明的袋子中，装有三个大小、质地都相同的乒乓球，球面上分别标有字母 $A$ 、 $O$ 、 $K$ ，搅匀后先从袋中任意摸出一个球，将对应字母记入图中的左边方格内；然后将球放回袋中搅匀，再从袋中任意摸出一个球，将对应字母记入图中的右边方格内.

(1)、求第一次摸到字母 $A$ 的概率；

(2)、用画树状图或列表等方法求两个方格中的字母从左往右恰好组成“ $O K$ ”的概率.

查看试题解析
22. 如图所示，在某海域，一艘指挥船在C处收到渔船在B处发出的求救信号，经确定，遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上，且BC＝80海里；指挥船搜索发现，在C处的南偏西60°方向上有一艘海监船A，恰好位于B处的正西方向.于是命令海监船A前往搜救，已知海监船A的航行速度为30海里/小时，问渔船在B处需要等待多长时间才能得到海监船A的救援？（结果精确到0.1小时）

查看试题解析
23. 如图，在△ABC中，∠ACB＝90°，点O在边BC上，以点O为圆心，OB为半径的⊙O交AB于点E，D为⊙O上一点，点B是弧DE中点.

(1)、如图1，若AE＝BE，求证：四边形ACDE是平行四边形；

(2)、如图2，若OB＝OC，BE＝2AE，求tan∠CAD的值.

查看试题解析
24. 某儿童服装经销商销售一种商品，经市场调查发现：该商品的一周销售量y（件）是售价x（元/件）的一次函数，其售价、一周销售量、一周销售利润w（元）的三组对应值如下表：

售价x（元/件）

50

60

一周销售量y（件）

100

80

一周销售利润w（元）

1000

1600

注：一周销售利润＝一周销售量×（售价﹣进价）

(1)、求y关于x的函数解析式；

(2)、该商品如何定价，才能使一周销售利润最大，最大利润是多少？

查看试题解析
25. 在△ABC中，AB＝6，BC＝5，AC＝4，D是线段AB上一点，且DB＝4，过点D作DE与线段AC相交于点E，使以A，D，E为顶点的三角形与△ABC相似，求DE的长.请根据下列两位同学的交流回答问题：

甲：过点D作DE∥BC，交AC于点E，则△ADE∽△ABC

∴ $\frac{D E}{B C} = \frac{A D}{D B}$

∴ $D E = \frac{A D}{D B} \cdot B C = \frac{A B - D B}{D B} \cdot B C = \frac{5}{2}$

乙：这个解答中有两个错误，其中一个是：比例式写错了！

(1)、写出正确的比例式及后续解答；

(2)、指出另一个错误，并给予正确解答.

查看试题解析

26. 2020年4月是我国第32个爱国卫生月.某校九年级通过网课举行了主题为“防疫有我，爱卫同行”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩（百分制）的情况，随机抽取了部分参赛学生的成绩，整理并绘制出如下不完整的统计表（表1）和统计图（如图）.请根据图表信息解答以下问题：

表1 知识竞赛成绩分组统计表

组别	分数/分	频数
A	60≤x＜70	a
B	70≤x＜80	10
C	80≤x＜90	14
D	90≤x＜100	18

(1)、本次调查一共随机抽取了个参赛学生的成绩；

(2)、表1中a＝；

(3)、所抽取的参赛学生的成绩的中位数落在的“组别”是；

(4)、统计图中B组所占的百分比是；

(5)、请你估计，该校九年级竞赛成绩达到80分以上（含80分）的学生人数：.

查看试题解析

27. 如图1，矩形ABCD中，∠ACB＝30°，将△ACD绕C点顺时针旋转α（0°＜α＜360°）至△A'CD'位置.

(1)、如图2，若AB＝2，α＝30°，求S_△BCD′.

(2)、如图3，取AA′中点O，连OB、OD′、BD′.若△OBD′存在，试判定△OBD′的形状.

(3)、当α＝α₁时，OB＝OD′，则α₁＝°；当α＝α₂时，△OBD′不存在，则α₂＝°.

查看试题解析

售价x（元/件）	50	60
一周销售量y（件）	100	80
一周销售利润w（元）	1000	1600