湖北省孝感市2021年数学中考调研试卷(4月)
试卷更新日期:2021-05-06 类型:中考模拟
一、单选题
-
1. 下列四个数中,最小的数是( )A、 B、0 C、1 D、22. 如图,有一块含有 角的直角三角板的两个顶点放在直尺的对边上.如果 ,那么 的度数是( )
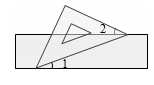 A、 B、 C、 D、3. 我国高铁通车总里程居世界第一,到2020年末,高铁总里程达到37900千米,37900用科学记数法表示为( )A、 B、 C、 D、4. 下面四个几何体中,俯视图为四边形的是( )A、
A、 B、 C、 D、3. 我国高铁通车总里程居世界第一,到2020年末,高铁总里程达到37900千米,37900用科学记数法表示为( )A、 B、 C、 D、4. 下面四个几何体中,俯视图为四边形的是( )A、 B、
B、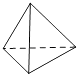 C、
C、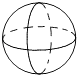 D、
D、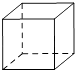 5. 下列计算正确的是( )A、 B、 C、 D、6. 某班篮球爱好小组10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成下表:
5. 下列计算正确的是( )A、 B、 C、 D、6. 某班篮球爱好小组10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成下表:投中次数
2
3
5
6
7
8
人数
1
2
3
2
1
1
则关于这10名队员投中次数组成的数据,下列说法错误的是( )
A、平均数为5 B、中位数为5 C、众数为5 D、方差为57. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形 的内角,正方形 变为菱形 ,若 ,则菱形 的面积与正方形 的面积之比是( ) A、 B、 C、 D、18. 如图,在 中, , , .动点P沿 从点A向点B移动(点P不与点A,点B重合),过点P作 的垂线,交折线 于点Q.记 , 的面积为y,则y关于x的函数图象大致是( )
A、 B、 C、 D、18. 如图,在 中, , , .动点P沿 从点A向点B移动(点P不与点A,点B重合),过点P作 的垂线,交折线 于点Q.记 , 的面积为y,则y关于x的函数图象大致是( ) A、
A、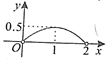 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 化简 .10. 如图,某水库堤坝横断面迎水坡AB的坡比是1: ,堤坝高BC=50m,则迎水坡面AB的长度是:.
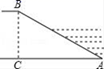 11. 已知方程 的两根为 ,则 .12. 如图,在 中, , , .进行如下操作:
11. 已知方程 的两根为 ,则 .12. 如图,在 中, , , .进行如下操作:①以点C为圆心,以 的长为半径画弧交 于点D;
②以点A为圆心,以 的长为半径画弧交 于点E.
则点E是线段 的黄金分割点.
根据以上操作, 的长为.
 13. 中华文化源远流长,文学方面:《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了解学生在寒假期间对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下两幅不完整的统计图:
13. 中华文化源远流长,文学方面:《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了解学生在寒假期间对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下两幅不完整的统计图: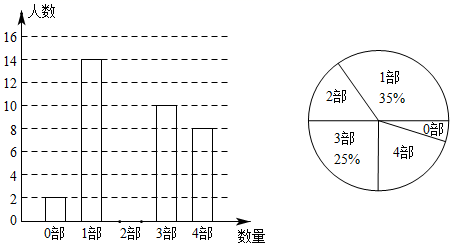
根据以上信息,本次调查所得数据中,扇形统计图中“读完了4部”所在扇形的圆心角为度;
14. 若x是不等式组 的整数解,则所有符合条件的x值的和为.15. 如图,平面直角坐标系中,已知 三个顶点的坐标分别为 , , ,将 沿x轴折叠得到 ,再将 绕原点O逆时针旋转 得到 ,则点 的对应点 的坐标为.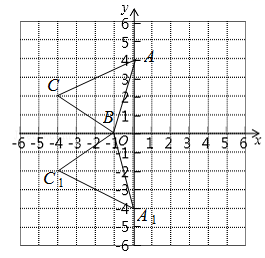 16. 我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”,它具有一定的规律性,从图中取一列数:1,3,6,10,…,分别记为 , , , ,…,那么 的值是.
16. 我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”,它具有一定的规律性,从图中取一列数:1,3,6,10,…,分别记为 , , , ,…,那么 的值是.
三、解答题
-
17. 计算: .18. 已知 ,求代数式 的值.19. 将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌子上.(1)、从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;(2)、先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.20. 如图,反比例函数 与一次函数 的图象在第一象限交于 、 两点.
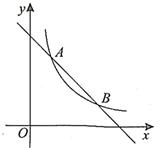 (1)、求反比例函数和一次函数的解析式;(2)、已知点 ,过点P作平行于y轴的直线,在第一象限内交一次函数 的图象于点M,交反比例函数 的图象于点N.若 ,结合函数图象直接写出a的取值范围.(3)、若Q为y轴上的一点,使 最小,求点Q的坐标.21. 如图, 为 的直径,点C为 上一点, 的平分线与 交于点D,与 交于点E.点F为 的延长线上一点,满足 .
(1)、求反比例函数和一次函数的解析式;(2)、已知点 ,过点P作平行于y轴的直线,在第一象限内交一次函数 的图象于点M,交反比例函数 的图象于点N.若 ,结合函数图象直接写出a的取值范围.(3)、若Q为y轴上的一点,使 最小,求点Q的坐标.21. 如图, 为 的直径,点C为 上一点, 的平分线与 交于点D,与 交于点E.点F为 的延长线上一点,满足 . (1)、求证: 与 相切;(2)、若 , ,求 的面积.22. 红星公司加大技术创新,研发出一种新产品,对新产品的生产和销售进行了规划.从2021年1月开始生产并销售该种产品,该种产品的生产成本为6万元/件,设第x( ,且x为整数)月份该种产品的售价为y万元/件,y与x之间的函数关系如图所示.
(1)、求证: 与 相切;(2)、若 , ,求 的面积.22. 红星公司加大技术创新,研发出一种新产品,对新产品的生产和销售进行了规划.从2021年1月开始生产并销售该种产品,该种产品的生产成本为6万元/件,设第x( ,且x为整数)月份该种产品的售价为y万元/件,y与x之间的函数关系如图所示.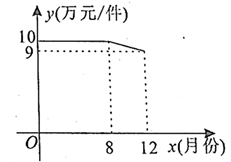 (1)、直接写出y与x之间的函数解析式,并写出自变量x的取值范围;(2)、第x月份生产并销售的产品数量为z件, ( ,且x为整数).该公司在第几月份所获的月利润最大?最大月利润为多少万元?23. 已知 和 都是等腰三角形,且 , .若点D在 边上运动时,总保持 ,连接 , 与 交于点F.
(1)、直接写出y与x之间的函数解析式,并写出自变量x的取值范围;(2)、第x月份生产并销售的产品数量为z件, ( ,且x为整数).该公司在第几月份所获的月利润最大?最大月利润为多少万元?23. 已知 和 都是等腰三角形,且 , .若点D在 边上运动时,总保持 ,连接 , 与 交于点F.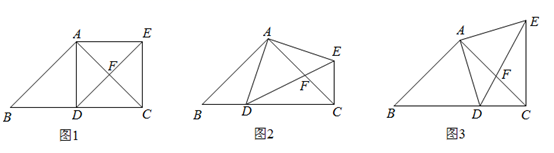 (1)、①如图1,当点D为 边中点时,求 的值;
(1)、①如图1,当点D为 边中点时,求 的值;②如图2,当点D不为 边中点时,求证: ;
(2)、如图3,当点D在 边上运动中恰好使得 时,若 , ,求 的长.24. 抛物线 经过点 和 ,与x轴交于另一点B.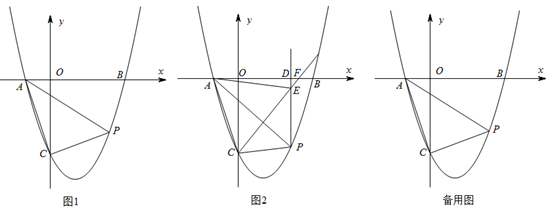 (1)、则抛物线的解析式为;(2)、点P为第四象限内抛物线上的点,连接 , , ,设点P的横坐标为 .
(1)、则抛物线的解析式为;(2)、点P为第四象限内抛物线上的点,连接 , , ,设点P的横坐标为 .①如图1,当 时,求 的值;
②如图2,过点P作x轴的垂线,垂足为点D,过点C作 的垂线,与射线 交于点E,与x轴交于点F.连接 ,当 时,求m的值.