湖北省武汉市2021年数学中考四模试卷(4月)
试卷更新日期:2021-05-06 类型:中考模拟
一、单选题
-
1. ﹣2的倒数是( )A、2 B、﹣2 C、 D、﹣2. 式子 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、3. “翻开数学书,恰好翻到第16页”,这个事件是( )A、随机事件 B、必然事件 C、不可能事件 D、确定事件4. 下列手机屏幕解锁图形案是轴对称图形的是( )A、
 B、
B、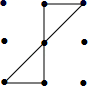 C、
C、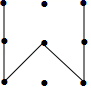 D、
D、 5. 如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是( )A、
5. 如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是( )A、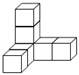 B、
B、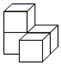 C、
C、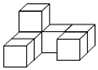 D、
D、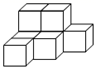 6. 如图所示的图形中,每个三角形上各有一个数字,若六个三角形上的数字之和为20,则称该图形是“和谐图形”.已知其中四个三角形上的数字之和为14,现从1,2,3,4,5中任取两个数字标在另外两个三角形上,则恰好使该图形为“和谐图形”的概率为( )
6. 如图所示的图形中,每个三角形上各有一个数字,若六个三角形上的数字之和为20,则称该图形是“和谐图形”.已知其中四个三角形上的数字之和为14,现从1,2,3,4,5中任取两个数字标在另外两个三角形上,则恰好使该图形为“和谐图形”的概率为( ) A、 B、 C、 D、7. 直线 与反比例函数 的图象交于两点 ,点 也在该反比例函数的图象上,则m,n,t的大小关系为( )A、 B、 C、 D、8. 如图,在四边形 中, , , , , .动点M,N同时从点A出发,点M以 的速度沿 向终点B运动,点N以 的速度沿折线 向终点C运动.设点N的运动时间为 , 的面积为 ,则下列图象能大致反映S与t之间函数关系的是( )
A、 B、 C、 D、7. 直线 与反比例函数 的图象交于两点 ,点 也在该反比例函数的图象上,则m,n,t的大小关系为( )A、 B、 C、 D、8. 如图,在四边形 中, , , , , .动点M,N同时从点A出发,点M以 的速度沿 向终点B运动,点N以 的速度沿折线 向终点C运动.设点N的运动时间为 , 的面积为 ,则下列图象能大致反映S与t之间函数关系的是( ) A、
A、 B、
B、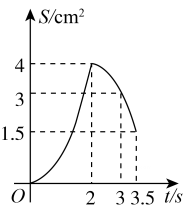 C、
C、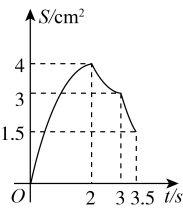 D、
D、 9. 观察下面倒“品”字形中各数之间的规律,根据观察到的规律得出a的值为( )
9. 观察下面倒“品”字形中各数之间的规律,根据观察到的规律得出a的值为( ) A、2020 B、2021 C、4040 D、403910. 如图, 是 的直径,C是 上一点,E是 的内心, .若 ,则 的面积为( )
A、2020 B、2021 C、4040 D、403910. 如图, 是 的直径,C是 上一点,E是 的内心, .若 ,则 的面积为( ) A、 B、2 C、 D、1
A、 B、2 C、 D、1二、填空题
-
11. 在学校的体育训练中,小杰同学投实心球的7次成绩就如统计图所示,则这7次成绩的中位数是 .
 12. 计算: 的结果是.13. 如图,E是 的边 上一点,将 沿 折叠,得到 交 于点F.若 , ,则 的度数为.
12. 计算: 的结果是.13. 如图,E是 的边 上一点,将 沿 折叠,得到 交 于点F.若 , ,则 的度数为. 14. 抛物线 (a,b,c为常数, )经过两点 ,下列四个结论:① ;②若点 在抛物线上,则 ;③ 的解集为 或 ;④方程 的两根为 .其中正确的结论是(填写序号).15. 如图,在锐角 中,D为 的中点,E为 上一点; 的延长线交于点F, , ,则 的长为.
14. 抛物线 (a,b,c为常数, )经过两点 ,下列四个结论:① ;②若点 在抛物线上,则 ;③ 的解集为 或 ;④方程 的两根为 .其中正确的结论是(填写序号).15. 如图,在锐角 中,D为 的中点,E为 上一点; 的延长线交于点F, , ,则 的长为.
三、解答题
-
16. 计算: .17. 如图, 和 相交于点 , , ,且 平分 ,求证: .
 18. 2020年3月,中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》.武汉市教育局发布了“普通中小学校劳动教育状况评价指标”.为了解某校学生一劳动次数的情况,随机抽取了若干学生进行调查,得到如图统计图表:
18. 2020年3月,中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》.武汉市教育局发布了“普通中小学校劳动教育状况评价指标”.为了解某校学生一劳动次数的情况,随机抽取了若干学生进行调查,得到如图统计图表: (1)、这次调查活动共抽取人, ;(2)、请将条形统计图补充完整;(3)、若该校学生总人数为3000人,根据调查结果,请你估计该校一周劳动4次及以上的学生人数.19. 如图,在 的正方形网格中,A,B,C,E均为小正方形的顶点,用无刻度的直尺画图,保留画图痕迹.
(1)、这次调查活动共抽取人, ;(2)、请将条形统计图补充完整;(3)、若该校学生总人数为3000人,根据调查结果,请你估计该校一周劳动4次及以上的学生人数.19. 如图,在 的正方形网格中,A,B,C,E均为小正方形的顶点,用无刻度的直尺画图,保留画图痕迹. (1)、将线段 绕点A逆时针旋转 得到线段 ;(2)、在 上画点T,使 ;(3)、在 上画点F(不与点C重合),使 ;(4)、在 上画点N,使 .20. 如图1, 的顶点A,B,C在 上, .
(1)、将线段 绕点A逆时针旋转 得到线段 ;(2)、在 上画点T,使 ;(3)、在 上画点F(不与点C重合),使 ;(4)、在 上画点N,使 .20. 如图1, 的顶点A,B,C在 上, .
 (1)、求证: 为 的切线;(2)、如图2, 与 交于点E,连接 .若 ,求 的值.21. 给出两种上宽带网的收费方式:
(1)、求证: 为 的切线;(2)、如图2, 与 交于点E,连接 .若 ,求 的值.21. 给出两种上宽带网的收费方式:收费方式
月使用费/元
包月上网时间/h
超时费/(元/ )
A
30
25
0.05
B
50
50
0.05
若每月上网时间 ,A,B两种上网的月收费分别为 元, 元.
(1)、直接写出 与x之间的函数关系式;(2)、x为何值时,两种收费方式一样?(3)、某用户选择B方式宽带网开网店.若该用户上网时间x小时,产生 (元)( )的经济收益.若某月该用户上网获得的利润最大值为5650元,直接写出a的值.(上网利润=上网经济收益-月宽带费)22.(1)、(问题背景)如图1,在 中,D为 上一点, ,求证: ;
 (2)、(变式迁移)
(2)、(变式迁移)如图2,在 中, ,D为 上一点, 交 于点E,连接 .求证: ;
(3)、(拓展迁移)如图3,在菱形 中,F为 上一点,E为 上一点, , ,直接写出 的长.
23. 已知抛物线 与x轴交于A,B两点(A在B的右侧),与y轴交于点C. (1)、直接写出A,B,C的坐标(可用含m的式子表示);(2)、如图1,若 ,P为第三象限内抛物线上的一点, ,求点P的横坐标;(3)、如图2,将抛物线向右平移n个单位 ,所得的抛物线与直线 交于M,N两点,且满足 ,点Q的坐标为 ,求 的最小值.
(1)、直接写出A,B,C的坐标(可用含m的式子表示);(2)、如图1,若 ,P为第三象限内抛物线上的一点, ,求点P的横坐标;(3)、如图2,将抛物线向右平移n个单位 ,所得的抛物线与直线 交于M,N两点,且满足 ,点Q的坐标为 ,求 的最小值.