湖北省武汉市2021年数学中考二模试卷（4月）

试卷更新日期：2021-05-06 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2020$ 的相反数是（）

A、2020 B、 $- 2020$ C、 $\frac{1}{2020}$ D、 $- \frac{1}{2020}$

查看试题解析
2. 若 $\sqrt{1 - 2 x}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x < \frac{1}{2}$ B、 $x < 2$ C、 $x \geq \frac{1}{2}$ D、 $x \leq \frac{1}{2}$

查看试题解析
3. 下列说法中，正确的是（）

A、“打开电视，正在播放湖北新闻节目”是必然事件 B、某种彩票中奖概率为10%是指买十张一定有一张中奖 C、“明天降雨的概率是50%表示明天有半天都在降雨” D、“掷一次骰子，向上一面的数字是2”是随机事件

查看试题解析
4. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图是由五个完全相同的小正方体组成的几何体，这个几何体的俯视图是（）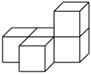

A、 B、 C、 D、

查看试题解析
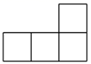6. 中考结束后，李哲，王浩两位同学都被某重点高中理科实验班录取，得知这个高中今年招收五个理科实验班，那么李哲，王浩分在同一理科实验班的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{2}$ C、 $\frac{1}{10}$ D、 $\frac{1}{4}$

查看试题解析
7. 反比例函数y $= \frac{k}{x}$ （x˂0）交等边△OAB于C、D两点，边长为5，OC＝3BD，则k的值（）

A、 $- \frac{9}{8} \sqrt{3}$ B、 $\frac{9}{4} \sqrt{3}$ C、 $\frac{15}{4} \sqrt{3}$ D、 $- \frac{15}{4} \sqrt{3}$

查看试题解析
8. 一个容器有进水管和出水管，每分钟的进水和出水是两个常数.从某时刻开始 $4 \min$ 内只进水不出水，从第 $4 \min$ 到第 $24 \min$ 内既进水又出水，从第 $24 \min$ 开始只出水不进水，容器内水量y（单位：L）与时间x（单位： $\min$ ）之间的关系如图所示，则图中a的值是（）

A、32 B、34 C、36 D、38

查看试题解析
9. 如图， $A B$ 为半圆O的直径， $B C ⊥ A B$ 且 $B C = A B$ ，射线 $B D$ 交半圆O的切线于点E， $D F ⊥ C D$ 交 $A B$ 于F，若 $A E = 2 B F ， D F = 2 \sqrt{10}$ ，则 $⊙ O$ 的半径长为（）

A、 $\frac{3 \sqrt{13}}{2}$ B、 $4 \sqrt{2}$ C、 $\frac{5 \sqrt{5}}{2}$ D、 $\frac{3 \sqrt{10}}{2}$

查看试题解析
10. 观察等式： $2 + 2^{2} = 2^{3} - 2$ ； $2 + 2^{2} + 2^{3} = 2^{4} - 2$ ； $2 + 2^{2} + 2^{3} + 2^{4} = 2^{5} - 2 \cdot \cdot \cdot$ 已知按一定规律排列的一组数： $2^{50}$ 、 $2^{51}$ 、 $2^{52}$ 、 $\cdot \cdot \cdot$ 、 $2^{99}$ 、 $2^{100}$ ．若 $2^{50} = a$ ，用含 $a$ 的式子表示这组数的和是（）

A、 $2 a^{2} - 2 a$ B、 $2 a^{2} - 2 a - 2$ C、 $2 a^{2} - a$ D、 $2 a^{2} + a$

查看试题解析

二、填空题

11. $\sqrt{{(- 5)}^{2}}$ = ．

查看试题解析
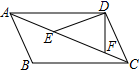
12. 疫情期间小童和爸爸妈妈爷爷奶奶测量体温结果分别为（单位：℃）：36.2、37.1、36.5、37.1、36.6，其中中位数是.

查看试题解析
13. 计算 $\frac{2}{m + n} - \frac{m - 3 n}{m^{2} - n^{2}}$ 的结果是.

查看试题解析
14. 如图，在 $▱ A B C D$ 中， $E$ 、 $F$ 是对角线 $A C$ 上两点， $A E = E F = C D$ ， $∠ A D F = 90 °$ ， $∠ B C D = 63 °$ ，则 $∠ A D E$ 的大小为

查看试题解析
15. 定义 $[a, b, c]$ 为函数 $y = a x^{2} + b x + c$ 的特征数，下面给出特征数为 $[2 m, 1 - m, - 1 - m]$ 的函数的一些结论：
①当 $m = - 3$ 时，函数图象的顶点坐标是 $(\frac{1}{3}, \frac{8}{3})$ ；

②当 $m > 0$ 时，函数图象截 $x$ 轴所得的线段长度大于 $\frac{3}{2}$ ；

③当 $m \leq 0$ 时，函数在 $x > \frac{1}{4}$ 时， $y$ 随 $x$ 的增大而减小；

④当 $m \neq 0$ 时，函数图象必经过两个定点.

其中正确的结论有.（填序号）

查看试题解析
16. 如图，在△ABC中，点D，E分别为AB，AC边上一点，且BE＝CD，CD⊥BE.若∠A＝30°，BD＝1，CE＝2 $\sqrt{3}$ ，则四边形CEDB的面积为.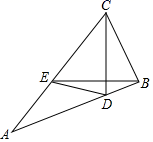

查看试题解析

三、解答题

17. 计算： $[a^{3} \cdot a^{5} + {(3 a^{4})}^{2}] \div a^{2}$ .

查看试题解析
18. 如图，点 $A$ 、 $B$ 、 $C$ 、 $D$ 在一条直线上， $C E$ 与 $B F$ 交于点 $G$ ， $∠ A = ∠ 1$ ， $C E ∥ D F$ ，求证： $∠ E = ∠ F$

查看试题解析
19. 某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况，随机调查了若干名学生，根据调查数据进行整理，绘制了如下的不完整统计图．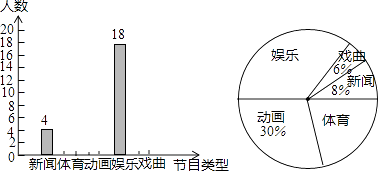
请你根据以上的信息，回答下列问题：

(1)、本次共调查了名学生，其中最喜爱戏曲的有人；在扇形统计图中，最喜爱体育的对应扇形的圆心角大小是．

(2)、根据以上统计分析，估计该校2000名学生中最喜爱新闻的人数．

查看试题解析
20. 以下各图均是由边长为1的小正方形组成的网格，图中的点A、B、C、D均在格点上．

(1)、在图①中，PC：PB＝．

(2)、利用网格和无刻度的直尺作图，保留痕迹，不写作法．
①如图②，在AB上找一点P ，使AP＝3．

②如图③，在BD上找一点P ，使△APB∽△CPD ．

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ C = 90 ° ， ∠ B A C$ 的平分线交 $B C$ 于点D，点O在 $A B$ 上，以 $O A$ 为半径的 $⊙ O$ 经过点D，与 $A B$ 交于点E.

(1)、求证： $B D^{2} = B E \cdot B A$ ；

(2)、若 $\cos B = \frac{2 \sqrt{2}}{3} ， A E = 4$ ，求 $C D$ .

查看试题解析

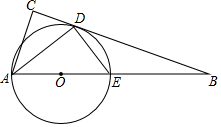22. 某商店销售一种商品，童威经市场调查发现：该商品的周销售量

y

（件）是售价

x

（元/件）的一次函数，其售价、周销售量、周销售利润

w

（元）的三组对应值如下表：

售价 $x$ （元/件）	50	60	80
周销售量 $y$ （件）	100	80	40
周销售利润 $w$ （元）	1000	1600	1600

注：周销售利润＝周销售量×（售价－进价）

(1)、①求

y

关于

x

的函数解析式（不要求写出自变量的取值范围）

②该商品进价是_▲_元/件；当售价是_▲_元/件时，周销售利润最大，最大利润是_▲_元

(2)、由于某种原因，该商品进价提高了

m

元/件

(m > 0)

，物价部门规定该商品售价不得超过65元/件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系.若周销售最大利润是1400元，求

m

的值

查看试题解析

23. 如图， $△ A B C$ 中， $C A = C B$

(1)、当点D为 $A B$ 上一点， $∠ A = \frac{1}{2} ∠ M D N = α$
①如图1，若点M、N分别在 $A C ､ B C$ 上， $A D = B D$ ，问： $D M$ 与 $D N$ 有何数量关系?证明你的结论；

②如图2，若 $\frac{A D}{B D} = \frac{1}{4}$ ，作 $∠ M D N = 2 α$ ，使点M在 $A C$ 上，点N在 $B C$ 的延长线上，完成图2，判断 $D M$ 与 $D N$ 的数量关系，并证明；

(2)、如图3，当点D为 $A C$ 上的一点， $∠ A = ∠ B D N = α ， C N / / A B ， C D = 2 ， A D = 1$ ，直接写出 $A B \cdot C N$ 的积.

查看试题解析
24. 在平面直角坐标系中，抛物线 $C_{1} ： y = a x^{2} + b x - 1$ 的最高点为点 $D (- 1 ， 0)$ ，将 $C_{1}$ 左移1个单位，上移1个单位得到拋物线 $C_{2}$ ，点P为 $C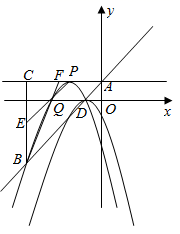_{2}$ 的顶点.

(1)、求抛物线C的解析式；

(2)、若过点D的直线l与抛物线 $C_{2}$ 只有一个交点，求直线l的解析式；

(3)、直线 $y = x + c$ 与抛物线 $C_{2}$ 交于D、B两点，交y轴于点A，连接 $A P$ ，过点B作 $B C ⊥ A P$ 于点C，点Q为 $C_{2}$ 上 $P B$ 之间的一个动点，连接 $P Q$ 交 $B C$ 于点E，连接 $B Q$ 并延长交 $A C$ 于点F，试说明： $F C \cdot (A C + E C)$ 为定值.

查看试题解析