湖北省黄石市大冶市三校2021年数学中考模拟联考试卷
试卷更新日期:2021-05-06 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、2021 B、 C、 D、2. 京剧脸谱、剪纸等图案一般蕴含着对称美,下列选取的图片中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是( )A、
3. 下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是( )A、 正方体
B、
正方体
B、 圆柱
C、
圆柱
C、 圆锥
D、
圆锥
D、 球
4. 下列计算正确的是( )A、a2•a3=a6 B、(ab2)2=ab4 C、(a+b)2=a2+b2 D、 =5. 要使式子 有意义,则m的取值范围是( )A、m≥﹣2,且m≠2 B、m≠2 C、m≥﹣2 D、m≥26. 方程组 的解为( )A、 B、 C、 D、7. 如图, 的斜边 在 轴上, ,将 绕原点顺时针旋转 ,则 的对应点 的坐标为( )
球
4. 下列计算正确的是( )A、a2•a3=a6 B、(ab2)2=ab4 C、(a+b)2=a2+b2 D、 =5. 要使式子 有意义,则m的取值范围是( )A、m≥﹣2,且m≠2 B、m≠2 C、m≥﹣2 D、m≥26. 方程组 的解为( )A、 B、 C、 D、7. 如图, 的斜边 在 轴上, ,将 绕原点顺时针旋转 ,则 的对应点 的坐标为( )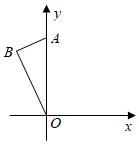 A、 B、 C、 D、8. 如图,在 中, , , , ,垂足为 , 的平分线交 于点 ,则 的长为( )
A、 B、 C、 D、8. 如图,在 中, , , , ,垂足为 , 的平分线交 于点 ,则 的长为( ) A、 B、 C、 D、9. 如图,AC是⊙O的弦,AC=4,点B是⊙O上的一个动点,且∠ABC=45°,若点M,N分别是AC,BC的中点,则MN的最大值为( )
A、 B、 C、 D、9. 如图,AC是⊙O的弦,AC=4,点B是⊙O上的一个动点,且∠ABC=45°,若点M,N分别是AC,BC的中点,则MN的最大值为( ) A、 B、4 C、6 D、10. 对于一个函数,自变量x取c时,函数值为0,则称c为这个函数的零点.若关于x的二次函数y=﹣x2﹣8x+m(m≠0)有两个不相等的零点x1 , x2(x1<x2),关于x的方程x2+8x﹣m﹣2=0有两个不相等的非零实数根x3 , x4(x3<x4),则下列式子一定正确的是( )A、0< <1 B、 >1 C、0< <1 D、 >1
A、 B、4 C、6 D、10. 对于一个函数,自变量x取c时,函数值为0,则称c为这个函数的零点.若关于x的二次函数y=﹣x2﹣8x+m(m≠0)有两个不相等的零点x1 , x2(x1<x2),关于x的方程x2+8x﹣m﹣2=0有两个不相等的非零实数根x3 , x4(x3<x4),则下列式子一定正确的是( )A、0< <1 B、 >1 C、0< <1 D、 >1二、填空题
-
11. 计算:(﹣π)0+( )﹣1﹣ sin60°=.12. 因式分解:x3y﹣4xy3= .13. 某种芯片每个探针单元的面积为0.00000164cm2 , 0.00000164用科学记数法表示为.14. 数据2,4,6,x,3,9的众数为3,则这组数据的中位数为.15. 如图,测高仪CD距建筑物底部5m,在测高仪D处观测建筑物顶端的仰角为50°,测高仪高度为1.5m,则建筑物AB的高度为m.(精确到0.1m,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
 16. 一个圆锥的底面半径r=5,高h=12,则这个圆锥的侧面积为.17. 如图,点A在y= (k>0)图象上,点B在x轴负半轴上,直线AB交y轴于C.若 = ,△AOB的面积为15,则k=.
16. 一个圆锥的底面半径r=5,高h=12,则这个圆锥的侧面积为.17. 如图,点A在y= (k>0)图象上,点B在x轴负半轴上,直线AB交y轴于C.若 = ,△AOB的面积为15,则k=. 18. 如图,在平面直角坐标系中,点P1的坐标为( , ),将线段OP1绕点O按顺时针方向旋转45°,再将其长度伸长为OP1的2倍,得到线段OP2;又将线段OP2绕O点按顺时针方向旋转45°,长度伸长为OP2的2倍,得到线段OP3;如此下去,得到线段OP4 , OP5 , …,OPn(n为正整数),则点P2022的坐标是.
18. 如图,在平面直角坐标系中,点P1的坐标为( , ),将线段OP1绕点O按顺时针方向旋转45°,再将其长度伸长为OP1的2倍,得到线段OP2;又将线段OP2绕O点按顺时针方向旋转45°,长度伸长为OP2的2倍,得到线段OP3;如此下去,得到线段OP4 , OP5 , …,OPn(n为正整数),则点P2022的坐标是.
三、解答题
-
19. 先化简,再求值:(1﹣ )÷( ),其中m=tan60°+3.20. 如图,在正方形 的外侧,作等边角形 ,连接 、 .
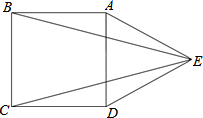 (1)、求证: ;(2)、求 的度数.21. 关于x的方程(k﹣1)x2﹣4x﹣1=0.(1)、若方程有实根,求k的取值范围;(2)、若方程两根x1 , x2 , 满足x12+x22﹣4x1x2=1,求k的值.22. 某单位食堂为全体960名职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)、求证: ;(2)、求 的度数.21. 关于x的方程(k﹣1)x2﹣4x﹣1=0.(1)、若方程有实根,求k的取值范围;(2)、若方程两根x1 , x2 , 满足x12+x22﹣4x1x2=1,求k的值.22. 某单位食堂为全体960名职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下: (1)、在抽取的240人中最喜欢A套餐的人数为 , 扇形统计图中“C”对应扇形的圆心角的大小为°;(2)、依据本次调查的结果,估计全体960名职工中最喜欢B套餐的人数;(3)、现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.23. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为提高学生的阅读品味,现决定购买获得第十届矛盾文学奖的《北上》(徐则臣著)和《牵风记》(徐怀中著)两种书共50本.已知购买2本《北上》和1本《牵风记》需100元;购买6本《北上》与购买7本《牵风记》的价格相同.(1)、求这两种书的单价;(2)、若购买《北上》的数量不少于所购买《牵风记》数量的一半,且购买两种书的总价不超过1600元.请问有哪几种购买方案?哪种购买方案的费用最低?最低费用为多少元?24. 如图,在△ABC中,点D是AC边上一点,以AD为直径的⊙O与边BC切于点E,且AB=BE.
(1)、在抽取的240人中最喜欢A套餐的人数为 , 扇形统计图中“C”对应扇形的圆心角的大小为°;(2)、依据本次调查的结果,估计全体960名职工中最喜欢B套餐的人数;(3)、现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.23. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为提高学生的阅读品味,现决定购买获得第十届矛盾文学奖的《北上》(徐则臣著)和《牵风记》(徐怀中著)两种书共50本.已知购买2本《北上》和1本《牵风记》需100元;购买6本《北上》与购买7本《牵风记》的价格相同.(1)、求这两种书的单价;(2)、若购买《北上》的数量不少于所购买《牵风记》数量的一半,且购买两种书的总价不超过1600元.请问有哪几种购买方案?哪种购买方案的费用最低?最低费用为多少元?24. 如图,在△ABC中,点D是AC边上一点,以AD为直径的⊙O与边BC切于点E,且AB=BE.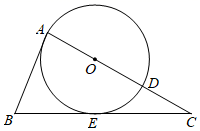 (1)、求证:AB是⊙O的切线;(2)、若BE=3,BC=7,求⊙O的半径长;(3)、求证: =CD•CA.25. 如图1,抛物线y=ax2+bx+ 与直线AB交于点A(﹣1,0),B(4, ),点D是抛物线上A,B之间的一个动点(不与A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
(1)、求证:AB是⊙O的切线;(2)、若BE=3,BC=7,求⊙O的半径长;(3)、求证: =CD•CA.25. 如图1,抛物线y=ax2+bx+ 与直线AB交于点A(﹣1,0),B(4, ),点D是抛物线上A,B之间的一个动点(不与A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD. (1)、求抛物线的解析式;(2)、设点D的横坐标为m,△ADB的面积为S,求S关于m的函数解析式,并求出当S取最大值时D点到AB的距离;(3)、利用图2在抛物线的对称轴上求点Q,使△ABQ为直角三角形.
(1)、求抛物线的解析式;(2)、设点D的横坐标为m,△ADB的面积为S,求S关于m的函数解析式,并求出当S取最大值时D点到AB的距离;(3)、利用图2在抛物线的对称轴上求点Q,使△ABQ为直角三角形.