湖北省黄冈市黄梅县2021年数学中考模拟试卷

试卷更新日期：2021-05-06 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣3的相反数为（）

A、﹣3 B、﹣ $\frac{1}{3}$ C、 $\frac{1}{3}$ D、3

查看试题解析
2. 石墨烯是最薄的纳米材料，其厚度为0.00000000034m，这个数字用科学记数法记为（）

A、 $3.4 \times 10^{- 10}$ B、 $3.4 \times 10^{- 9}$ C、 $0.34 \times 10^{- 9}$ D、 $0.34 \times 10^{- 10}$

查看试题解析
3. 下列运算正确的是（）

A、 $a \cdot a^{2} = a^{2}$ B、 ${(a b)}^{3} = a b^{3}$ C、 $a^{10} \div a^{2} = a^{5}$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
4.
如图所示的几何体，其主视图是（　　）

A、 B、 C、 D、

查看试题解析
5. 已知一元二次方程x²－2x－1＝0的两根分别为x₁ ， x₂ ，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值为（）

A、2 B、－1 C、－ $\frac{1}{2}$ D、－2

查看试题解析
6. 如图，已知直线AB//CD，∠GEB 的平分线EF交CD于点F，∠1＝30°，则∠2等于（）

A、135° B、145° C、155° D、165°

查看试题解析
7. 如图，在直角坐标系中，将矩形OABC沿OB对折，使点A落在点D处，已知 $O A = \sqrt{3} ， A B = 1$ ，则点D的坐标为（）

A、 $(\frac{\sqrt{3}}{2} ， \frac{3}{2})$ B、 $(\frac{\sqrt{3}}{2} ， 3)$ C、 $(\frac{3}{2} ， \frac{\sqrt{3}}{2})$ D、 $(\frac{1}{2} ， \frac{\sqrt{3}}{2})$

查看试题解析
8. 如图中的图象（折线ABCDE）描述了一汽车在某一直道上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系．根据图中提供的信息，给出下列说法：
①汽车共行驶了120千米；

②汽车在行驶途中停留了0.5小时；

③汽车在整个行驶过程中的平均速度为 $\frac{160}{3}$ 千米/时；

④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少．

其中正确的说法有（　　）

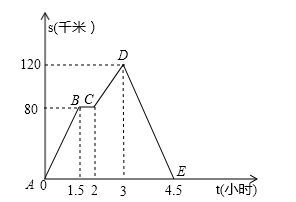A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 函数y= $\frac{\sqrt{2-x}}{x + 1}$ 中，自变量x的取值范围是.

查看试题解析
10. 计算： $| 1 - \sqrt{3} | - 3 \tan 30^{\circ} + {(2018 - π)}^{0}$ =.

查看试题解析
11. 把 $9 x y^{3} - x y$ 因式分解的结果是.

查看试题解析
12. 一组从小到大排列的数据：2，5，x，y，2x，11的平均数与中位数都是7，则x-y=.

查看试题解析
13. 若一个圆锥的底面圆的周长是4 $π$ cm，母线长是6cm，则该圆锥的侧面展开图的圆心角的度数是度.

查看试题解析
14. a如图，矩形OABC中，点A、C分别在x轴，y轴的正半轴上，且 $O A = \sqrt{3} ， A B = 1$ ，点P为线段OA上一动点，则 $\frac{1}{2} O P + P B$ 最小值为.

查看试题解析
15. 如图，反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象经过△ABD的顶点A，B，交BD于点C，AB经过原点，点D在y轴上，若BD＝4CD，△OBD的面积为15，则k的值为.

查看试题解析
16. 在直角坐标系中，点A的坐标为 $(3 ， 0)$ ，若抛物线 $y = x^{2} - 2 x + n - 1$ 与线段 $O A$ 有且只有一个公共点，则n的取值范围为．

查看试题解析

三、解答题

17. 解一元一次不等式组： ${\begin{matrix} - 5 x + 3 > 3 (x - 2) \\ \frac{x + 1}{2} \leq 1 - \frac{5 - x}{6} \end{matrix}$

查看试题解析
18. 先化简，再求值： $(a + \frac{1}{a - 2}) \div (a + 2 + \frac{3}{a - 2})$ ，其中 $a = \sqrt{2} - 1$

查看试题解析
19. 如图，菱形ABCD的对角线AC、BD相交于点O， $B E // A C$ ， $A E // B D$ ，OE与AB交于点F.

(1)、求证：四边形AEBO的为矩形；

(2)、若OE＝10，AC＝16，求菱形ABCD的面积.

查看试题解析
20. 某种肺炎病毒在A国爆发，经世卫组织研究发现：病毒有极强的传染性，一个病毒携带者与10个人有密切接触，其中的6人会感染病毒，成为新的病毒携带者.在调查某工厂的疫情时，发现最初只有1位出差回来的病毒携带者，在召开工厂车间组长会议时发生了第一轮传染，开完会后所有人都回到各自车间工作又发生了第二轮传染，这时全厂一共有169人检测出携带病毒.假如每个病毒携带者每次的密切接触者人数都相同，求每个病毒携带者每次的密切接触了多少人？

查看试题解析
21. 现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）：
步数
频数
频率
0≤x＜4000
8
a
4000≤x＜8000
15
0.3
8000≤x＜12000
12
b
12000≤x＜16000
c
0.2
16000≤x＜20000
3
0.06
20000≤x＜24000
d
0.04
请根据以上信息，解答下列问题：

(1)、写出a，b，c，d的值并补全频数分布直方图；

(2)、本市约有37800名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？

(3)、若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步的两名教师与大家分享心得，求被选取的两名教师恰好都在20000步（包含20000步）以上的概率．

查看试题解析
22. 数学活动课上，小明和小红要测量小河对岸大树BC的高度，小红在点A测得大树顶端B的仰角为45°，小明从A点出发沿斜坡走3 $\sqrt{5}$ 米到达斜坡上点D，在此处测得树顶端点B的仰角为31°，且斜坡AF的坡比为1：2.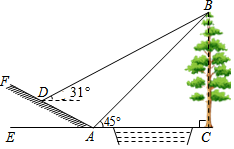

(1)、求小明从点A到点D的过程中，他上升的高度；

(2)、依据他们测量的数据能否求出大树BC的高度？若能，请计算；若不能，请说明理由.（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）

查看试题解析
23. 如图，AB是⊙O的直径，C是弧AB的中点，延长AC至D，使CD＝AC，连接DB.E是OB的中点，CE的延长线交DB的延长线于点F，AF交⊙O于点H，连接BH.

(1)、求证：BD是⊙O的切线；

(2)、⊙O的直径为2，求BH的长.

查看试题解析
24. 绿色生态农场生产并销售某种有机产品，每日最多生产130kg，假设生产出的产品能全部售出，每千克的销售价y₁（元）与产量x（kg）之间满足一次函数关系y₁＝﹣ $\frac{3}{5}$ x+168，生产成本y₂（元）与产量x（kg）之间的函数图象如图中折线ABC所示.

(1)、求生产成本y₂（元）与产量x（kg）之间的函数关系式；

(2)、求日利润为W（元）与产量x（kg）之间的函数关系式；

(3)、当产量为多少kg时，这种产品获得的日利润最大？最大日利润为多少元？

查看试题解析
25. 如图1，抛物与 y=ax²+bx+4（a＜0）与x轴交于点 $A (- 1 ， 0)$ ， $B (4 ， 0)$ ，与 $y$ 轴交于点C

(1)、求该抛物线对应的函数表达式，并写出其顶点M的坐标

(2)、试在y轴上找一点T，使得TM⊥TB，求T点的坐标

(3)、如图2，连接BC，点D是直线BC上方抛物线上的点，连接OD、CD，OD交BC于点F，当 $S_{Δ C O F} ： S_{Δ C D F} = 4 ： 3$ 时，求点D的坐标

(4)、如图3，点E的坐标为（0，-2），点P是抛物线上的动点，连接EB，PB，PE形成的△PBE中，是否存在点P，使得∠PBE或∠PEB等于2∠OBE？若存在，请直接写出符合条件的P点坐标；若不存在，请说明理由

查看试题解析

步数	频数	频率
0≤x＜4000	8	a
4000≤x＜8000	15	0.3
8000≤x＜12000	12	b
12000≤x＜16000	c	0.2
16000≤x＜20000	3	0.06
20000≤x＜24000	d	0.04