甘肃省天水市张家川县2021年数学中考模拟试卷(3月)
试卷更新日期:2021-05-06 类型:中考模拟
一、单选题
-
1. 如果a与﹣6互为倒数,那么a是( )A、﹣6 B、6 C、﹣ D、2. 某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )A、 B、 C、 D、3. 如图是某个几何体的展开图,该几何体是( )
 A、三棱柱 B、四棱柱 C、圆柱 D、圆锥4. 如图,将直尺与三角尺叠放在一起,如果 ,那么 的度数为( )
A、三棱柱 B、四棱柱 C、圆柱 D、圆锥4. 如图,将直尺与三角尺叠放在一起,如果 ,那么 的度数为( )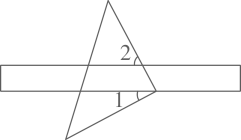 A、62° B、56° C、28° D、72°5. 已知a+b=4,则代数式 的值为( )A、3 B、1 C、0 D、-16. 不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )A、 B、 C、 D、7. 等腰Rt△ABO在平面直角坐标系中的位置如图所示,已知点A(﹣2,0),AB=BO,则点B的坐标为( )
A、62° B、56° C、28° D、72°5. 已知a+b=4,则代数式 的值为( )A、3 B、1 C、0 D、-16. 不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )A、 B、 C、 D、7. 等腰Rt△ABO在平面直角坐标系中的位置如图所示,已知点A(﹣2,0),AB=BO,则点B的坐标为( ) A、(﹣1,1) B、(﹣1,2) C、(1,﹣1) D、(﹣1,﹣2)8. 若 ,则正比例函数 与反比例函数 在同一平面直角坐标系中的大致图象可能是( )A、
A、(﹣1,1) B、(﹣1,2) C、(1,﹣1) D、(﹣1,﹣2)8. 若 ,则正比例函数 与反比例函数 在同一平面直角坐标系中的大致图象可能是( )A、 B、
B、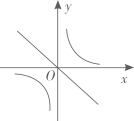 C、
C、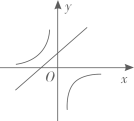 D、
D、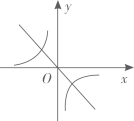 9. 如图,点A,B,C,D在⊙O上,BC=DC,若∠BOD=124°,则∠A的大小为( )
9. 如图,点A,B,C,D在⊙O上,BC=DC,若∠BOD=124°,则∠A的大小为( ) A、27° B、31° C、56° D、63°10. 全民健身的今天,散步是大众喜欢的运动.甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行.甲乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是( )
A、27° B、31° C、56° D、63°10. 全民健身的今天,散步是大众喜欢的运动.甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行.甲乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是( ) A、80米/分,40米/分 B、80米/分,60米/分 C、60米/分,40米/分 D、120米/分,80米/分
A、80米/分,40米/分 B、80米/分,60米/分 C、60米/分,40米/分 D、120米/分,80米/分二、填空题
-
11. 在函数y= 中,自变量x的取值范围是.12. 方程 的解为.13. 若关于x的一元一次不等式组 有2个整数解,则a的取值范围是.14. 若一组数据2,3,x,1,5,7的众数为7,则这组数据的中位数为.15. 若关于x的一元二次方程x2+mx+2n=0有一个根是2,则m+n= .16. 用一个半径为30,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半轻是.17. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为.
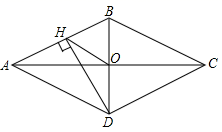 18. 有2021个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.若第一个数是0,第二个数是1,则这2021个数的和是.
18. 有2021个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.若第一个数是0,第二个数是1,则这2021个数的和是.三、解答题
-
19.(1)、计算:﹣14﹣| ﹣1|+( ﹣1.414)0+2sin60°﹣(﹣ )﹣1.(2)、先化简,再求值:(x+2+ )÷ ,其中x= ﹣1.20. 某校对九年级学生进行“综合素质”评价,评价的结果分为A(优秀)、B(良好)、C(合格)、D(不合格)四个等级,现从中随机抽查了若干名学生的“综合素质”等级作为样本进行数据处理,并绘制以下两幅不完整的统计图.
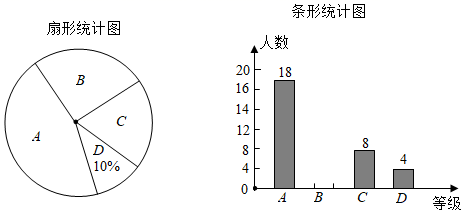
请根据统计图提供的信息,解答下列问题:
(1)、请补充完整条形统计图;(2)、B(良好)等级人数所占百分比是;(3)、在扇形统计图中,C(合格)等级所在扇形的圆心角度数是°;(4)、若该校九年级学生共1000名,估算评价结果为A等级或B等级的学生共有多少名?21. 如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y= (k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.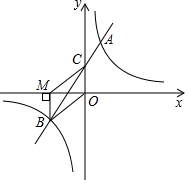 (1)、求反比例函数和一次函数的解析式.(2)、连接OB,MC,求四边形MBOC的面积.22. 如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC的高度,他们先在A处测得建筑物顶端B的仰角为60°,然后从A处后退40m到达D处,在D处测得建筑物顶端B的仰角是30°,点D、A、C在同一水平线上,BC⊥DC.
(1)、求反比例函数和一次函数的解析式.(2)、连接OB,MC,求四边形MBOC的面积.22. 如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC的高度,他们先在A处测得建筑物顶端B的仰角为60°,然后从A处后退40m到达D处,在D处测得建筑物顶端B的仰角是30°,点D、A、C在同一水平线上,BC⊥DC.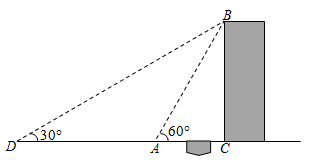 (1)、求∠DBC的度数;(2)、求建筑物BC的高.(参考数据: ≈1.414, ≈1.732)23. 如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作O⊙,与BC交于点M,与AB的另一个交点为E,过M作MN⊥AB,垂足为N.
(1)、求∠DBC的度数;(2)、求建筑物BC的高.(参考数据: ≈1.414, ≈1.732)23. 如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作O⊙,与BC交于点M,与AB的另一个交点为E,过M作MN⊥AB,垂足为N.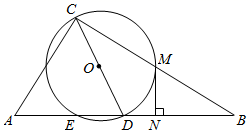 (1)、求证:MN是⊙O的切线;(2)、若⊙O的直径为5,sinB= ,求ED的长.24. 小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周销售数量 (本)与销售单价 (元)之间满足一次函数关系,三对对应值如下表:
(1)、求证:MN是⊙O的切线;(2)、若⊙O的直径为5,sinB= ,求ED的长.24. 小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周销售数量 (本)与销售单价 (元)之间满足一次函数关系,三对对应值如下表:销售单价 (元)
12
14
16
每周的销售量 (本)
500
400
300
(1)、求 与 之间的函数关系式;(2)、通过与其他网店对比,小红将这款笔记本的单价定为 元( ,且 为整数),设每周销售该款笔记本所获利润为 元,当销售单价定为多少元时每周所获利润最大,最大利润是多少元?25. 定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.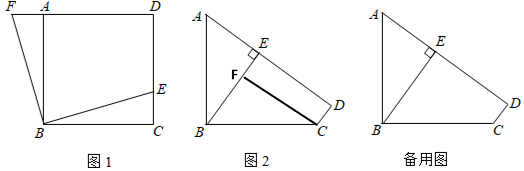
根据以上定义,解决下列问题:
(1)、如图1,正方形ABCD中E是CD上的点,将△BCE绕B点旋转,使BC与BA重合,此时点E的对应点F在DA的延长线上,则四边形BEDF填(“是”或“不是”)“直等补”四边形;(2)、如图2,已知四边形ABCD是“直等补”四边形,AB=BC=5,CD=1,AD>AB,过点B作BE⊥AD于E.①过C作CF⊥BF于点F,试证明:BE=DE,并求BE的长;
②若M是AD边上的动点,求△BCM周长的最小值.
26. 如图,抛物线y=ax2+bx+4(a≠0)与x轴交于点A(﹣1,0)和点B(4,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.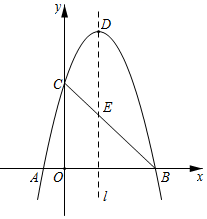 (1)、求抛物线的表达式;(2)、点P是第一象限内抛物线上的动点,连接PB,PC,若S△PBC= S△ABC , 求点P的坐标;(3)、点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M,使得以点M,N,E为顶点的三角形与△OBC相似?若存在,直接写出点M的坐标;若不存在,说明理由.
(1)、求抛物线的表达式;(2)、点P是第一象限内抛物线上的动点,连接PB,PC,若S△PBC= S△ABC , 求点P的坐标;(3)、点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M,使得以点M,N,E为顶点的三角形与△OBC相似?若存在,直接写出点M的坐标;若不存在,说明理由.