河南省许昌市禹州市2021届九年级下学期数学第二次月考试卷
试卷更新日期:2021-05-06 类型:月考试卷
一、单选题
-
1. 的相反数是( )A、8 B、-8 C、 D、2. 2020年12月10日,国家统计局发布的数据显示,2020年全国粮食总产量为13390亿斤,比上年增加113亿斤,增长0.9%,粮食生产再获丰收,产量连接6年保持在1.3万亿斤以上.将数据“13390亿”用科学记数法可表示为( )A、 B、 C、 D、3. 一个几何体是由7个完全相同的小正方体搭建而成的.若它的俯视图如图所示,则它的左视图不可能是( )
 A、
A、 B、
B、 C、
C、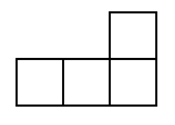 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,是一个含 角的三角形放在一个菱形纸片上,且斜边与菱形的一边平行,则 的度数是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,是一个含 角的三角形放在一个菱形纸片上,且斜边与菱形的一边平行,则 的度数是( ) A、 B、 C、 D、6. 2020年10月25日,孙琳参加学校举办的“抗美援朝70周年缅怀先烈”主题演讲比赛,她的演讲资料、语言表达、形象风度、综合印象得分分别为85分,70分,80分,80分.若依次按照40%,40%,15%,5%的百分比确定成绩,则她的成绩是( )A、 80分 B、79分 C、78分 D、77分7. 由于疫情的原因,拥有“中国医疗耗材之都”之称的河南长垣这个冬天特别的忙!其中某医护用品集团计划生产口罩1500万只,实际每天比原计划多生产2000只,结果提前五天完成任务,则原计划每天生产多少万只口罩?设原计划每天生产 万只口罩,根据题意可列方程为( )A、 B、 C、 D、8. 关于 的一元二次方程 有两个实数根,则 的取值范围为( )A、 且 B、 且 C、 D、9. 如图,已知 的顶点 , 分别在 轴, 轴上, , ,按以下步骤作图:①分别以点 , 为圆心,大于 的长为半径作弧,交于点 , ;②作直线 交 轴于点 ,交 轴于点 ,则点 的坐标为( )
A、 B、 C、 D、6. 2020年10月25日,孙琳参加学校举办的“抗美援朝70周年缅怀先烈”主题演讲比赛,她的演讲资料、语言表达、形象风度、综合印象得分分别为85分,70分,80分,80分.若依次按照40%,40%,15%,5%的百分比确定成绩,则她的成绩是( )A、 80分 B、79分 C、78分 D、77分7. 由于疫情的原因,拥有“中国医疗耗材之都”之称的河南长垣这个冬天特别的忙!其中某医护用品集团计划生产口罩1500万只,实际每天比原计划多生产2000只,结果提前五天完成任务,则原计划每天生产多少万只口罩?设原计划每天生产 万只口罩,根据题意可列方程为( )A、 B、 C、 D、8. 关于 的一元二次方程 有两个实数根,则 的取值范围为( )A、 且 B、 且 C、 D、9. 如图,已知 的顶点 , 分别在 轴, 轴上, , ,按以下步骤作图:①分别以点 , 为圆心,大于 的长为半径作弧,交于点 , ;②作直线 交 轴于点 ,交 轴于点 ,则点 的坐标为( ) A、 B、 C、 D、10. 如图,在菱形 中, , ,点 , 在直线 上,且点 的坐标为 .将菱形 绕原点 逆时针旋转,每次旋转 ,则第85次旋转结束时,点 的坐标为( )
A、 B、 C、 D、10. 如图,在菱形 中, , ,点 , 在直线 上,且点 的坐标为 .将菱形 绕原点 逆时针旋转,每次旋转 ,则第85次旋转结束时,点 的坐标为( )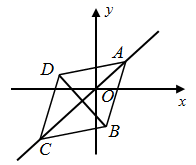 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知实数 在数轴上的对应点如图所示,计算: .
 12. 不等式组 的最小整数解为.13. 在一个不透明的空袋子里,放入分别标有数字1,3,4,5的四个小球(除数字外其他完全相同),从中随机摸出2个小球,摸到的2个小球的数字之和恰为偶数的概率是.14. 如图,在 中, , , .以点 为圆心, 的长为半径画弧,分别交 , 于点 , ,以点 为圆心, 的长为半径为画弧,交 于点 ,交 于点 ,则图中阴影部分的面积为.
12. 不等式组 的最小整数解为.13. 在一个不透明的空袋子里,放入分别标有数字1,3,4,5的四个小球(除数字外其他完全相同),从中随机摸出2个小球,摸到的2个小球的数字之和恰为偶数的概率是.14. 如图,在 中, , , .以点 为圆心, 的长为半径画弧,分别交 , 于点 , ,以点 为圆心, 的长为半径为画弧,交 于点 ,交 于点 ,则图中阴影部分的面积为. 15. 如图,在等边三角形 中, , , 分别为边 和 上的点,连接 ,将 沿 折叠得到 .若点 始终落在边 上,则线段 的取值范围为.
15. 如图,在等边三角形 中, , , 分别为边 和 上的点,连接 ,将 沿 折叠得到 .若点 始终落在边 上,则线段 的取值范围为.
三、解答题
-
16. 先化简,再求值: ,其中 .17. 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,对两条流水线上的产品进行抽样调查,随机从每条流水线上各抽取20 件产品称出它们的质量 (单位:g),规定质量在 范围内的产品为合格产品.将所得数据进行收集整理,部分信息如下:
a.甲、乙两条流水线的产品质量的频数分布表如下:
质量/g
甲
1
1
3
12
2
1
乙
2
2
2
10
3
1
b.甲流水线的产品质量在“ ”这一组的数据如下:
400 400 400 400 400 401 401 402 402 402 403 404
c.根据甲、乙两条流水线的产品质量数据,得到的统计量如下:

平均数
中位数
方差
合格率
甲
401
25.5
75%
乙
401
401
36.1
请根据以上信息,回答下列问题:
(1)、 , .(2)、综合上表中的统计量,你认为哪个流水线的产品生产情况较好?请从两个方面说明理由.(3)、若该食品厂现需要用甲流水线生产1600件产品,请估计这批产品中质量合格的有多少件.18. 如图,在等腰直角三角形 , ,以 为直径作 ,点 是边 上的一点,连接 ,过点 作 于点 ,交 于点 ,交 于点 ,过点 作 的切线交 的延长线于点 ,连接 , .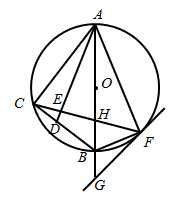 (1)、求证: .(2)、若 的直径为 , ,求出 的面积.19. 2020年11月10日,“雪龙2”起航!中国第37次南极考察队从上海出发,执行南极考察任务.已知“雪龙2”船上午9时在 市的南偏东 方向上的点 处,且在 岛的北偏东 方向上,已知B市在 岛的北偏东 方向上,且距离 岛248 km.此时,“雪龙2”船沿着AC方向以25 km/h的速度运动,请你计算“雪龙2”船大约几点钟到达 岛?(结果精确到1 km.参考数据: , , , )
(1)、求证: .(2)、若 的直径为 , ,求出 的面积.19. 2020年11月10日,“雪龙2”起航!中国第37次南极考察队从上海出发,执行南极考察任务.已知“雪龙2”船上午9时在 市的南偏东 方向上的点 处,且在 岛的北偏东 方向上,已知B市在 岛的北偏东 方向上,且距离 岛248 km.此时,“雪龙2”船沿着AC方向以25 km/h的速度运动,请你计算“雪龙2”船大约几点钟到达 岛?(结果精确到1 km.参考数据: , , , ) 20. 为方便教师利用多媒体进行教学,某学校计划采购 , 两种类型的激光翻页笔.已知购买2支 型激光翻页笔和4支 型激光翻页共需180元;购买4支 型激光翻页笔和2支 型激光翻页笔共需210元.(1)、求 , 两种类型激光翻页笔的单价.(2)、学校准备采购 , 两种类型的激光翻页笔共60支,且 型激光翻页笔的数量不少于 型激光翻页笔数量的2倍,请设计出最省钱的购买方案,并说明理由.21. 如图,抛物线 交 轴于 , 两点,交 轴于点 ,直线 与抛物线交于点 , ,与 轴交于点 ,连接 , .
20. 为方便教师利用多媒体进行教学,某学校计划采购 , 两种类型的激光翻页笔.已知购买2支 型激光翻页笔和4支 型激光翻页共需180元;购买4支 型激光翻页笔和2支 型激光翻页笔共需210元.(1)、求 , 两种类型激光翻页笔的单价.(2)、学校准备采购 , 两种类型的激光翻页笔共60支,且 型激光翻页笔的数量不少于 型激光翻页笔数量的2倍,请设计出最省钱的购买方案,并说明理由.21. 如图,抛物线 交 轴于 , 两点,交 轴于点 ,直线 与抛物线交于点 , ,与 轴交于点 ,连接 , .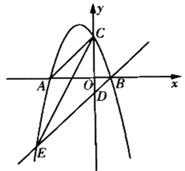 (1)、求抛物线的解析式和直线 的解析式.(2)、点 是直线 上方抛物线上一点.若 ,求此时点 的坐标.22. 如图1,在菱形 中, ,某数学兴趣小组从函数的角度对菱形 的对角线长度进行如下探究:
(1)、求抛物线的解析式和直线 的解析式.(2)、点 是直线 上方抛物线上一点.若 ,求此时点 的坐标.22. 如图1,在菱形 中, ,某数学兴趣小组从函数的角度对菱形 的对角线长度进行如下探究: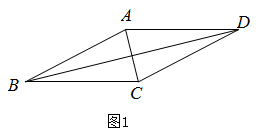
利用几何画板,测量出以下几组值:
1.00
2.00
3.00
4.00
5.00
6.00
7.00
8.00
9.00
9.54
9.80
9.95
9.95
9.80
9.54
9.16
8.66
8.00
7.14
4.36
3.00
2.00
1.00
根据所学的函数知识,对上述数据进行分析.
(1)、表格中 的值为.(2)、设 的长为自变量 , 的长是关于自变量 的函数,记为 ,现已在图2所示的平面直角坐标系中描出了表格中各组数据的对应点 .
①请画出函数 的图象;
②请在同一平面直角坐标系中画出直线 ,结合所绘制的函数图象,写出函数 的一条性质.
(3)、在平面直角坐标系中,将三角板(含 角的直角三角板)按如图3所示方式放置,顶点和坐标原点重合,斜边在 轴上.画出射线 .若 与绘制的函数图象交于点 ,则此时菱形 的面积为. 23. 将等边三角形 的边绕 绕点 逆时针旋转至 ,记旋转角为 .连接 ,过点 作 垂直于直线 ,垂足为 ,连接 ,取 边的中点 ,连接 .(1)、如图1,当 时, 的度数为 ,连接 ,可求出 的值为.
23. 将等边三角形 的边绕 绕点 逆时针旋转至 ,记旋转角为 .连接 ,过点 作 垂直于直线 ,垂足为 ,连接 ,取 边的中点 ,连接 .(1)、如图1,当 时, 的度数为 ,连接 ,可求出 的值为.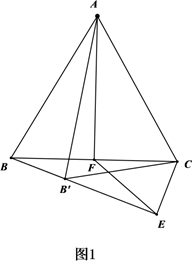
 (2)、当 且 时,
(2)、当 且 时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当 , , 三点共线时,请直接写出 的值.
