初中数学苏科版八年级下册9.4 正方形的性质和判定 同步训练
试卷更新日期:2021-05-05 类型:同步测试
一、单选题
-
1. 以下命题中正确的是( )A、对角线相等的平行四边形是正方形 B、对角线互相垂直的平行四边形是正方形 C、对角线相等且互相平分的四边形是正方形 D、对角线相等且互相垂直平分的四边形是正方形2. 如图,正方形ABCD的面积为8,菱形AECF的面积为4,则EF的长是( )
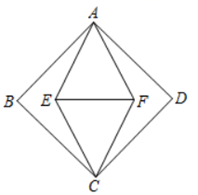 A、4 B、 C、2 D、13. 边长分别为2和4的两个正方形按如图的样式摆放并连线,则图中阴影部分的面积为( )
A、4 B、 C、2 D、13. 边长分别为2和4的两个正方形按如图的样式摆放并连线,则图中阴影部分的面积为( ) A、6 B、7 C、8 D、124. 如图,正方形 的边长为 , , ,连接 ,则线段 的长为( )
A、6 B、7 C、8 D、124. 如图,正方形 的边长为 , , ,连接 ,则线段 的长为( ) A、 B、 C、 D、5. 如图,在正方形ABCD中,BD=2,∠DCE是正方形ABCD的外角,P是∠DCE的角平分线CF上任意一点,则△PBD的面积等于( )
A、 B、 C、 D、5. 如图,在正方形ABCD中,BD=2,∠DCE是正方形ABCD的外角,P是∠DCE的角平分线CF上任意一点,则△PBD的面积等于( ) A、1 B、1.5 C、2 D、2.56. 正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FC过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( )
A、1 B、1.5 C、2 D、2.56. 正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FC过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( ) A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变7. 如图,正方形 和正方形 中,点D在 上, , ,H是 的中点,那么 的长是( )
A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变7. 如图,正方形 和正方形 中,点D在 上, , ,H是 的中点,那么 的长是( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中有一边长为
A、 B、 C、 D、8. 如图,在平面直角坐标系中有一边长为 的正方形
的正方形 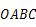 ,边
,边  ,
,  分别在
分别在  轴、
轴、 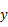 轴上,如果以对角线
轴上,如果以对角线  为边作第二个正方形
为边作第二个正方形  ,再以对角线
,再以对角线  为边作第三个正方形
为边作第三个正方形  ,照此规律作下去,则点 的坐标为( )
,照此规律作下去,则点 的坐标为( )  A、 B、 C、 D、9. 在正方形ABCD中,点E为BC边的中点,点 与点B关于AE对称, 与AE交于点F,连接 , , 下列结论: ; 为等腰直角三角形; ; 其中正确的是( )
A、 B、 C、 D、9. 在正方形ABCD中,点E为BC边的中点,点 与点B关于AE对称, 与AE交于点F,连接 , , 下列结论: ; 为等腰直角三角形; ; 其中正确的是( ) A、 B、 C、 D、10. 如图,在正方形ABCD中,AC、BD相交于点O,E、F分别为BC、CD上的两点,BE=CF,AE、BF分别交BD、AC于M、N两点,连OE、OF.下列结论:①AE=BF;②AE⊥BF;③CE+CF=BD;④S四边形OECF= S正方形ABCD , 其中正确的是( )
A、 B、 C、 D、10. 如图,在正方形ABCD中,AC、BD相交于点O,E、F分别为BC、CD上的两点,BE=CF,AE、BF分别交BD、AC于M、N两点,连OE、OF.下列结论:①AE=BF;②AE⊥BF;③CE+CF=BD;④S四边形OECF= S正方形ABCD , 其中正确的是( ) A、①② B、①④ C、①②④ D、①②③④
A、①② B、①④ C、①②④ D、①②③④二、填空题
-
11. 如图,正方形 的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且 ,则四边形 的面积为 .
 12. 如图,两个正方形的边长分别为 、 ,若 , ,则四边形 (阴影部分)的面积为
12. 如图,两个正方形的边长分别为 、 ,若 , ,则四边形 (阴影部分)的面积为 13. 如图,在正方形 中,直线 分别过 三点且 ,若 与 的距离为 , 与 的距离为 ,则正方形 的边长是 .
13. 如图,在正方形 中,直线 分别过 三点且 ,若 与 的距离为 , 与 的距离为 ,则正方形 的边长是 . 14. 如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是cm.
14. 如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是cm. 15. 如图,在正方形ABCD中,P为对角线BD上一点,过P作PE⊥BC于E,PF⊥CD于F,若PE=1,PF=3,则AP= 。
15. 如图,在正方形ABCD中,P为对角线BD上一点,过P作PE⊥BC于E,PF⊥CD于F,若PE=1,PF=3,则AP= 。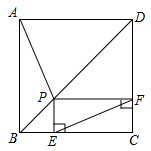 16. 如图,矩形纸片 中,已知 , ,点 在 边上,沿 折叠纸片,使点 落在点 处,连结 ,当 为直角三角形时, 的长为.
16. 如图,矩形纸片 中,已知 , ,点 在 边上,沿 折叠纸片,使点 落在点 处,连结 ,当 为直角三角形时, 的长为. 17. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为2的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=4 EF,则正方形ABCD的面积为
17. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为2的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=4 EF,则正方形ABCD的面积为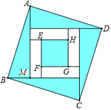 18. 如图,边长为2的正方形ABCD中,AE平分∠DAC , AE交CD于点F , CE⊥AE , 垂足为点E , EG⊥CD , 垂足为点G , 点H在边BC上,BH=DF , 连接AH、FH , FH与AC交于点M , 以下结论:①FH=2BH;②AC⊥FH;③S△ACF=1;④CE= AF;⑤EG2=FG•DG , 其中正确结论的有(只填序号).
18. 如图,边长为2的正方形ABCD中,AE平分∠DAC , AE交CD于点F , CE⊥AE , 垂足为点E , EG⊥CD , 垂足为点G , 点H在边BC上,BH=DF , 连接AH、FH , FH与AC交于点M , 以下结论:①FH=2BH;②AC⊥FH;③S△ACF=1;④CE= AF;⑤EG2=FG•DG , 其中正确结论的有(只填序号).
三、解答题
-
19. 如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合), ,且 .求证:四边形ABCD是正方形.
 20. 正方形ABCD和正方形CEFG的边长分别为b和a将它们如图所示放置,求图中阴影部分的面积.
20. 正方形ABCD和正方形CEFG的边长分别为b和a将它们如图所示放置,求图中阴影部分的面积. 21. 如图,正方形ABCD的对角线AC,BD相交于点O.E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OG=OE.
21. 如图,正方形ABCD的对角线AC,BD相交于点O.E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OG=OE.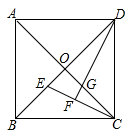 22. 如图,边长为2的正方形ABCD中,P是对角线AC上的一个动点(点P不与A、C重合),连结BP,过点B作 且使得 ,连结QP交BC于点E,延长QP与直线AD交于点F.
22. 如图,边长为2的正方形ABCD中,P是对角线AC上的一个动点(点P不与A、C重合),连结BP,过点B作 且使得 ,连结QP交BC于点E,延长QP与直线AD交于点F. (1)、 面积的最小值为;(2)、连结CQ,求证: ;(3)、猜想PF与EQ的数量关系,并说明理由.23. 如图(1),正方形 的对角线 相交于点 是 上一点,连接 过点A作 垂足为 与 相交于点F.
(1)、 面积的最小值为;(2)、连结CQ,求证: ;(3)、猜想PF与EQ的数量关系,并说明理由.23. 如图(1),正方形 的对角线 相交于点 是 上一点,连接 过点A作 垂足为 与 相交于点F.
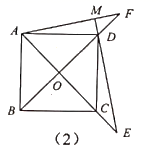 (1)、直接写出 与 的数量关系;(2)、如图(2)若点E在 的延长线上, 于点 交 的延长线于点F,其他条件不变.试探究 与 的数量关系,并说明理由.24. 如图①, 的顶点P在正方形 两条对角线的交点处, ,将 绕点P旋转,旋转过程中 的两边分别与正方形 的边 和 交于点E和点F(点F与点C、D不重合).
(1)、直接写出 与 的数量关系;(2)、如图(2)若点E在 的延长线上, 于点 交 的延长线于点F,其他条件不变.试探究 与 的数量关系,并说明理由.24. 如图①, 的顶点P在正方形 两条对角线的交点处, ,将 绕点P旋转,旋转过程中 的两边分别与正方形 的边 和 交于点E和点F(点F与点C、D不重合). (1)、如图①,当 时, 、 、 之间满足的数量关系是;(2)、如图②,将图①中的正方形 改为 的菱形,其他条件不变,当 时,(1)中的结论变为 ,并给出证明过程;
(1)、如图①,当 时, 、 、 之间满足的数量关系是;(2)、如图②,将图①中的正方形 改为 的菱形,其他条件不变,当 时,(1)中的结论变为 ,并给出证明过程; (3)、在(2)的条件下,若旋转过程中 的边 与边 的延长线交于点E,其他条件不变,探究在整个运动变化过程中, 、 、 之间满足的数量关系,直接写出结论,不用加以证明.
(3)、在(2)的条件下,若旋转过程中 的边 与边 的延长线交于点E,其他条件不变,探究在整个运动变化过程中, 、 、 之间满足的数量关系,直接写出结论,不用加以证明. 25. 如图1,点E是正方形ABCD边AB上任意一点,以BE为边作正方形BEFG , 连接DF , 点M , N分别是线段AE、DF中点,连接MN .
25. 如图1,点E是正方形ABCD边AB上任意一点,以BE为边作正方形BEFG , 连接DF , 点M , N分别是线段AE、DF中点,连接MN . (1)、请猜想MN与AE的关系,并证明你的结论;(2)、把图1中的正方形BEFG绕点B顺时针旋转 ,此时点E、G恰好分别落在线段BC、AB上,如图2,其他条件不变,(1)中的结论是否成立?请说明理由.
(1)、请猜想MN与AE的关系,并证明你的结论;(2)、把图1中的正方形BEFG绕点B顺时针旋转 ,此时点E、G恰好分别落在线段BC、AB上,如图2,其他条件不变,(1)中的结论是否成立?请说明理由.