初中数学苏科版八年级下册9.5 三角形的中位线 同步训练
试卷更新日期：2021-05-05 类型：同步测试
一、单选题
-
1. Rt△ABC两直角边的长分别为6cm和8cm，则连接这两条直角边中点的线段长为（ ）A、10cm B、3cm C、4cm D、5cm2. 如图，在△ABC中，点D、E、F分别是BC、AB、AC的中点，如果△ABC的周长为20，那么△DEF的周长是（ ）
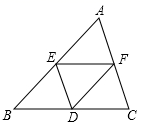A、20 B、15 C、10 D、53. 如图，Rt△ABC中，∠BAC＝90°，点D ， E分别是边AB ， BC的中点，AD与CE交于点F ， 则△DEF与△ACF的面积之比是（ ）
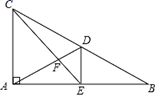A、1：2 B、1：3 C、2：3 D、1：44. 如图，在△ABC中，D是AB上一点，AD＝AC，AE⊥CD，垂足为点E，F是BC的中点，若BD＝16，则EF的长为（ ）
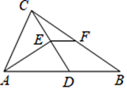A、32 B、16 C、8 D、45. 如图，在平行四边形ABCD中，已知 分别是线段OD，OA的中点，则EF的长为（ ）
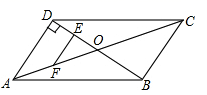A、3 B、4 C、5 D、86. 如图，在四边形ABCD中，∠C＝90°，E，F分别为AB，AD的中点，BC＝2，CD＝ ，则EF的长为（ ）
A、 B、 C、 D、7. 如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，则应添加的条件是（ ）
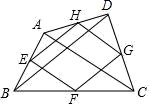A、AB//CD B、AC⊥BD C、AC=BD D、AD=BC8. 如图，在正方形ABCD中，AB＝4，E是CD的中点，将 BCE沿BE翻折至 BFE，连接DF，则DF的长度是（ ）
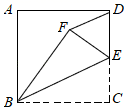A、 B、 C、 D、9. 矩形ABCD与CEFG，如图放置，点B，C，E共线，点C，D，G共线，连结AF，取AF的中点H，连结GH，若BC=EF=4，CD=CE=2，则GH=（ ）
A、1 B、 C、 D、10. 如图，在图（1）中，A1、B1、C1分别是△ABC的边BC、CA、AB的中点，在图（2）中，A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点，…，按此规律，则第n个图形中平行四边形的个数共有（ ）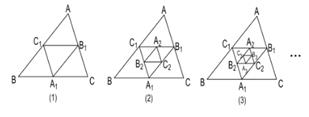
A、3个 B、4n个 C、3n个 D、3n个二、填空题
-
11. 如图，矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是BO、BC的中点，若AB=5，BC=12，则EF=；
12. 如图，在△ABC中，点D在BC上，BD=AB，BM⊥AD于点M，N是AC的中点，连接MN。若AB=5，BC=8，则MN=。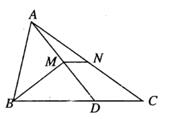
13. 如图所示， 为 的中位线，点F在 上，且 ，若 则 的长为.
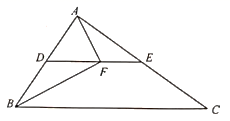14. 如图， ABC中，AB＝AC=4，以AC为斜边作Rt ADC，使∠ADC＝90°，∠CAD＝∠CAB＝30°，E、F分别是BC、AC的中点，则ED＝.
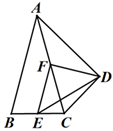15. 如图，已知△ABC中，点M是BC边上的中点，AN平分∠BAC，BN⊥AN于点N，若AB＝8，MN＝2，则AC的长为.
16. 如图，在四边形ABCD中，AD＝BC ， ∠DAB＝50°，∠CBA＝70°，P、M、N分别是AB ， AC、BD的中点，若BC＝8，则△PMN的周长是 ．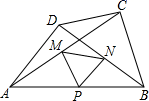
17. 如图，△ABC的周长为26，点D、 E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P.若BC=10，则PQ的长是.
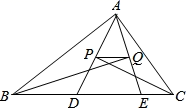18. 在Rt△ABC中，∠C=90°，AC=3，BC=4，点N是BC边上一点，点M为AB边上的动点，点D、E分别为CN、MN的中点，则DE长度的取值范围是.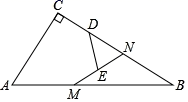
三、解答题
-
19. 如图，在△ABC中，∠ACB＝90°，点D ， E ， F分别为AB ， AC ， BC的中点.求证：CD＝EF ．
20. 如图，△ABC中，AB=8，AC=6，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，求线段EF的长．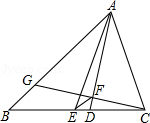
21. 已知：如图，在四边形 中， ， 为对角线 的中点， 为 的中点， 为 的中点.求证：
22. 如图，在平行四边形ABCD中，EF∥AB且交BC于点E，交AD于点F，连接AE、BF交于点M，连接CF、DE交于点N，连接MN.试探讨MN与AD的大小关系和位置关系，并加以证明.
23. 如图，D是△ABC内一点，连接DB、DC、DA ， 并将AB、DB、DC、AC的中点E、H、G、F依次连接，得到四边形EHGF ．
(1)、求证：四边形EHGF是平行四边形；(2)、若BD⊥CD ， AD＝7，BD＝8，CD＝6，求四边形EHGF的周长．24. 已知：四边形ABCD，E，F，G，H是各边的中点．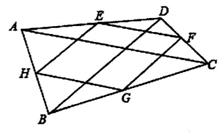
(1)、求证：四边形EFGH是平行四边形；(2)、假如四边形ABCD是一个矩形，猜想四边形EFGH是什么图形？并证明你的猜想。25. 如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN.
(1)、求证：BM=MN；(2)、∠BAD=60°，AC平分∠BAD，AC=2，求BN的长.26. 如图，点O是△ABC内一点，连接OB、OC，线段AB、OB、OC、AC的中点分别为D、E、F、G.
(1)、判断四边形DEFG的形状，并说明理由；(2)、若M为EF的中点，OM=2，∠OBC和∠OCB互余，求线段BC的长.27. 如图，在R△ABC中，∠ACB=90°，点F是CB的中点，过点F作FE∥AC交AB于点E点D是CA延长线上的一点，且AD= AC，连接DE、AF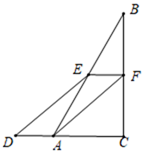
(1)、求证：四边形ADEF是平行四边形；(2)、若四边ADEF的周长是24cm，BC的长为6cm，求四边形ADEF的面积.28. 在菱形ABCD中，∠BAD＝60°
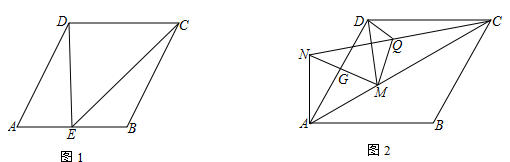(1)、如图1，点E为线段AB的中点，连接DE、CE.若AB＝4，求线段EC的长(2)、如图2，M为线段AC上一点（不与A、C重合），以AM为边向上构造等边三角形AMN，线段MN与AD交于点G，连接NC、DM，Q为线段NC的中点，连接DQ、MQ，判断DM与DQ的数量关系，并证明你的结论(3)、在(2)的条件下，若AC＝ ，请你直接写出DM＋CN的最小值