初中数学苏科版八年级下册10.4 分式的乘除 同步训练
试卷更新日期:2021-05-05 类型:同步测试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 计算 的结果是( )A、x+1 B、 C、 D、3. 化简 的结果是( )A、 B、 C、 D、4. 计算 的结果为( )A、 B、 C、 D、5. 如图,在数轴上表示 的值的点是( )
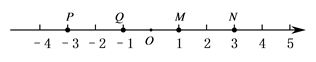 A、点 B、点 C、点 D、点6. 计算 的结果是( )A、 B、 C、 D、7. 若代数式 ,那么代数式M为( )A、 B、 C、 D、8. 已知m²-m=7,则 的值为( )A、3 B、 2 C、4 D、59. 若先化简 ,再求值,且 是满足 的整数,则化简求值的结果为( )A、0或 或-2或4 B、-2或 C、-2 D、10. 如图1,设 ,则有( ).
A、点 B、点 C、点 D、点6. 计算 的结果是( )A、 B、 C、 D、7. 若代数式 ,那么代数式M为( )A、 B、 C、 D、8. 已知m²-m=7,则 的值为( )A、3 B、 2 C、4 D、59. 若先化简 ,再求值,且 是满足 的整数,则化简求值的结果为( )A、0或 或-2或4 B、-2或 C、-2 D、10. 如图1,设 ,则有( ). A、0<k< B、 <k<1 C、1<k<2 D、k>2
A、0<k< B、 <k<1 C、1<k<2 D、k>2二、填空题
-
11. 计算: = .12. 化简 的结果是.13. 当y=3x时,计算 的结果等于 .14. 化简: 的结果是.15. 已知x2-4x+4与 互为相反数,则式子 ÷(x+y)的值为 .16. 已知:x:y:z=2:3:4,则 的值为.17. 已知 ,则简 的值等于 .
18. 已知实数a,b,c满足 ,则 .三、解答题
-
19. 先化简,再求值: ,其中 .20. 先化简,再求值: ,其中 取-1、+1、-2、-3中你认为合理的数.21. 先化简,再求值: ¸ +2m,其中m是方程x2-x-5=0的根.22. 先化简,再求值: ,其中x的值从不等式组 的整数解中选取.23. 以下是小明化简分式 的过程.
解:原式
①
②
③
④
(1)、小明的解答过程在第步开始出错;(2)、请你帮助小明写出正确的解答过程,并计算当 时分式的值.24. 化简 并解答:(1)、当 时,求原代数式的值;(2)、原代数式的值能等于-1 吗?为什么?25. 已知分式 A =(1)、化简这个分式;(2)、当 a>2 时,把分式 A 化简结果的分子与分母同时加上 4 后得到分式 B,问:分式 B 的值较原来分式 A 的值是变大了还是变小了?试说明理由;(3)、若A的值是整数,且 a 也为整数,求出符合条件的所有 a 值的和.26. 已知 , , .(1)、当 , , 时,求 的值;(2)、当 时,求 的值.27. 在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知: ,求代数式x2+ 的值.
解:∵ ,∴ =4
即 =4∴x+ =4∴x2+ =(x+ )2﹣2=16﹣2=14
材料二:在解决某些连等式问题时,通常可以引入参数“k”,将连等式变成几个值为k的等式,这样就可以通过适当变形解决问题.
例:若2x=3y=4z,且xyz≠0,求 的值.
解:令2x=3y=4z=k(k≠0)
则
根据材料回答问题:
(1)、已知 ,求x+ 的值.(2)、已知 ,(abc≠0),求 的值.(3)、若 ,x≠0,y≠0,z≠0,且abc=7,求xyz的值.28. 如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”.(1)、下列分式:① ;② ;③ ;④ .其中是“和谐分式”是(填写序号即可);(2)、若a为正整数,且 为“和谐分式”,请写出a的值;(3)、在化简 时,小东和小强分别进行了如下三步变形:
小东:原式= = = ,
小强:原式= = ,
显然,小强利用了其中的和谐分式,第三步所得结果比小东的结果简单,说出原因,
请你接着小强的方法完成化简.