初中数学苏科版八年级下册11.3 用反比例函数解决问题 同步训练
试卷更新日期:2021-05-05 类型:同步测试
一、单选题
-
1. 一定质量的二氧化碳,当它的体积V=5 , 密度ρ=1.98kg/ 时,p与V 之间的函数关系式是( )。A、p=9.9V B、 C、 D、2. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )A、不小于0.5m3 B、不大于0.5m3 C、不小于0.6m3 D、不大于0.6m33. 如图,曲线表示温度T(℃)与时间t(h)之间的函数关系,它是一个反比例函数的图象的一支.当温度T≤2℃时,时间t应( )
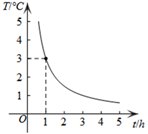 A、不小于 h B、不大于 h C、不小于 h D、不大于 h4. 如图,直线y=-x+3与y轴交于点A,与反比例函数y= (k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )
A、不小于 h B、不大于 h C、不小于 h D、不大于 h4. 如图,直线y=-x+3与y轴交于点A,与反比例函数y= (k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )
 A、y= B、y=- C、y= D、y=-5. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y= (k≠0)的一部分,则当x=16时,大棚内的温度为( )
A、y= B、y=- C、y= D、y=-5. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y= (k≠0)的一部分,则当x=16时,大棚内的温度为( ) A、18℃ B、15.5℃ C、13.5℃ D、12℃6. 如图,在平面直角坐标系中,直线y=﹣ x+1分别交x轴,y轴于点A,B,交反比例函数y1= (k<0,x<0),y2= (k<0,x>0)于点C,D两点,连接OC,OD,过点D作DE⊥x轴于点E,若△ODE的面积与△OCB的面积相等,则k的值是( )
A、18℃ B、15.5℃ C、13.5℃ D、12℃6. 如图,在平面直角坐标系中,直线y=﹣ x+1分别交x轴,y轴于点A,B,交反比例函数y1= (k<0,x<0),y2= (k<0,x>0)于点C,D两点,连接OC,OD,过点D作DE⊥x轴于点E,若△ODE的面积与△OCB的面积相等,则k的值是( )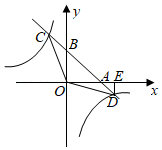 A、﹣4 B、﹣2 C、﹣2 D、﹣7. 如图,在平面直角坐标系中,点 、 在函数 的图象上.当 时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D . QD交PA于点E . 随着m的增大,四边形ACQE的面积( )
A、﹣4 B、﹣2 C、﹣2 D、﹣7. 如图,在平面直角坐标系中,点 、 在函数 的图象上.当 时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D . QD交PA于点E . 随着m的增大,四边形ACQE的面积( )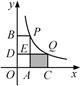 A、减小 B、增大 C、先减小后增大 D、先增大后减小8. 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )
A、减小 B、增大 C、先减小后增大 D、先增大后减小8. 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )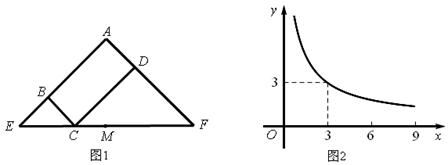 A、当x=3时,EC<EM B、当y=9时,EC>EM C、当x增大时,EC·CF的值增大。 D、当y增大时,BE·DF的值不变。9. 如图,A,B两点在反比例函数 的图象上,C,D两点在反比例函数 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则 的值是( )
A、当x=3时,EC<EM B、当y=9时,EC>EM C、当x增大时,EC·CF的值增大。 D、当y增大时,BE·DF的值不变。9. 如图,A,B两点在反比例函数 的图象上,C,D两点在反比例函数 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则 的值是( )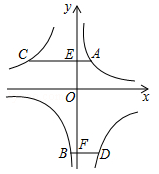 A、6 B、4 C、3 D、210. 如图,在直角坐标系中,直线 与坐标轴交于A、B两点,与双曲线 ( )交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
A、6 B、4 C、3 D、210. 如图,在直角坐标系中,直线 与坐标轴交于A、B两点,与双曲线 ( )交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:① ;②当0<x<3时, ;③如图,当x=3时,EF= ;④当x>0时, 随x的增大而增大, 随x的增大而减小.其中符合题意结论的个数是( )
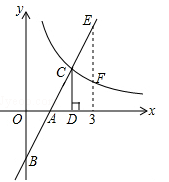 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
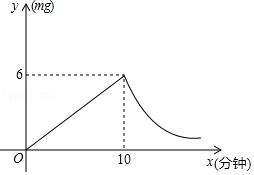
11. 在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,P=50,则当P=25时,V= .12. 某水池容积为300m3 , 原有水100m3 , 现以xm3/min的速度匀速向水池中注水,注满水需要y min,则y关于x的函数表达式为 .13. 小刚欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为900牛顿和0.5米,则当动力臂为1.5米时,撬动石头需要的力大于牛顿.(提示根据杠杆原理:阻力x阻力臂=动力x动力臂)14. 一次函数y1=k1x(k1≠0)与反比例函数y2= (k2≠0)的图象的一个交点是M(-3,2),若y2<y1<5,则x的取值范围是 。15. 已知直线 与反比例函数 的图象交于A、B两点,当线段AB的长最小时,以AB为斜边作等腰直角三角形△ABC,则点C的坐标是 .16. 为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为6mg.研究表明当每立方米空气中含药量低于1.2mg时,对人体方能无毒害作用,那么从消毒开始,至少需要经过分钟后,学生才能回到教室.
三、综合题
-
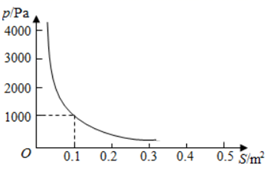
17. 已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为ν(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时)(1)、求v关于t的函数表达式(2)、若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?18. 码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.(1)、轮船到达目的地开始卸货,平均卸货速度v(单位:吨/天)与卸货天数t之间有怎样的函数关系?(2)、由于遇到紧急情况,要求船上货物不超过5天卸货完毕,那么平均每天至少要缷货多少吨?19. 记面积为 的平行四边形的一条边长为x(cm),这条边上的高线长为y(cm).(1)、求y关于x的函数表达式,以及自变量x的取值范围.(2)、求当边长满足 时,高线长的最大值.20. 某校绿色行动小组组织一批人参加植树活动,完成任务的时间y(h)是参加植树人数 (人)的反比例函数,且当 人时, .(1)、若平均每人每小时植树4棵,则这次共计要植树棵;(2)、当 时,求y的值;(3)、为了能在 内完成任务,至少需要多少人参加植树?21. 某气球内充满一定质量的气体,当温度不变时,气球内气体的压强p(kPa)与气体的体积v(m³)成反比例。当气体的体积V=0.8m3时,气球内气体的压强p=112.5kPa。当气球内气体的压强大于150kPa时,气球就会爆炸。(1)、求p关于V的函数表达式。(2)、当气球内气体的体积从1.2m³增加至1.8 m³ (含1.2 m³和1.8m³)时,求气体压强的范围。(3)、若气球内气体的体积为0.55m³,气球会不会爆炸?请说明理由。22. 在压力不变的情况下,某物体所受到的压强p(Pa)与它的受力面积S(m2)之间成反比例函数关系,其图象如图所示.
 (1)、求p与S之间的函数表达式;(2)、当S=0.4 m2时,求该物体所受到的压强p.23. 某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/小时),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题:
(1)、求p与S之间的函数表达式;(2)、当S=0.4 m2时,求该物体所受到的压强p.23. 某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/小时),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题: (1)、这场沙尘暴的最高风速是多少?最高风速维持了多长时间;(2)、求出当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系?(3)、在这次沙尘暴的形成过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻是“危险时刻”.问这次风暴的整个过程中,“危险时刻”一共有多长时间?24. 病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.
(1)、这场沙尘暴的最高风速是多少?最高风速维持了多长时间;(2)、求出当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系?(3)、在这次沙尘暴的形成过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻是“危险时刻”.问这次风暴的整个过程中,“危险时刻”一共有多长时间?24. 病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.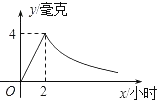 (1)、求当0≤x≤2时,y与x的函数关系式;(2)、求当x>2时,y与x的函数关系式;(3)、若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?25. 制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为
(1)、求当0≤x≤2时,y与x的函数关系式;(2)、求当x>2时,y与x的函数关系式;(3)、若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?25. 制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为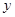 (℃),从加热开始计算的时间为
(℃),从加热开始计算的时间为  (分钟).据了解,该材料加热时,温度
(分钟).据了解,该材料加热时,温度 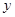 与时间
与时间  成一次函数关系;停止加热进行操作时,温度
成一次函数关系;停止加热进行操作时,温度 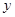 与时间
与时间  成反比例关系(如图8所示).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
成反比例关系(如图8所示).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.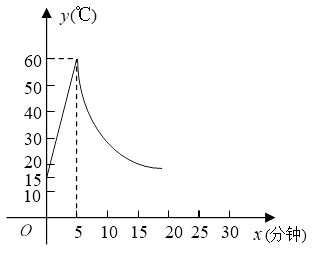 (1)、分别求出将材料加热和停止加热进行操作时,
(1)、分别求出将材料加热和停止加热进行操作时, 与
与  的函数关系式; (2)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停
的函数关系式; (2)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
26. 为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg , 请你根据题中提供的信息,解答下列问题: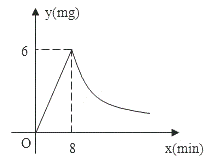 (1)、药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?(2)、研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?(3)、研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
(1)、药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?(2)、研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?(3)、研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?