初中数学苏科版七年级下册12.3 互逆命题 同步训练
试卷更新日期:2021-05-05 类型:同步测试
一、单选题
-
1. 下列说法正确的是( )A、每个定理都有逆定理 B、真命题的逆命题都是真命题 C、每个命题都有逆命题 D、假命题的逆命题都是假命题2. 命题“锐角小于90°的逆命题是( ).
A、如果这个角是锐角,那么这个角小于90° B、不是锐角的角不小于90° C、不小于90 ° 的角不是锐角 D、小于90° 的角是锐角3. 下列命题中,逆命题正确的是( )A、全等三角形的对应边相等 B、全等三角形的对应角相等 C、全等三角形的周长相等 D、全等三角形的面积相等4. 下列命题的逆命题不正确的是( )A、若 ,则 B、两直线平行,内错角相等 C、等腰三角形的两个底角相等 D、对顶角相等5. 下列命题的逆命题为真命题的是( )A、对顶角相等 B、如果x=3,那么|x|=3 C、直角都相等 D、内错角相等,两直线平行6. 下列各命题的逆命题是真命题的是( ).A、对顶角相等 B、等边三角形是锐角三角形 C、如果两个数同号,那么它们的积是正数 D、如果两个数都是负数,那么它们的和为负数7. 下列命题中,①同旁内角互补,两直线平行;②若a>1且b>1,则a+b>2;③直角都相等;④直角三角形的两锐角互余.它们的逆命题是真命题的个数是( ).A、1 B、2 C、3 D、4二、填空题
-
8. 命题“不是对顶角的两个角不相等”的逆命题是.9. 命题“等边三角形的三个内角相等”的逆命题是.10. 直角三角形两锐角互余的逆命题是.11. 命题“等角的余角相等”的逆命题是命题.12. 命题“如果两个角是直角,那么它们相等”的逆命题是命题(填“真”或“假”).13. 命题“如果两个角的和为180° ,那么这两个角互补”的逆命题是.
14. 命题“如果a>b,那么ac>bc”的逆命题是.15. 试写出命题“直角三角形的两个锐角互余”的逆命题: .16. “相等的角是对顶角”的逆命题是命题(填“真”或“假”).17. 命题“对顶角相等”的逆命题是一个命题(填“真”或“假”).18. 命题“如果 a=b ,那么| a | = | b | ”的逆命题是。
三、综合题
-
19. 下列各组命题是否是互逆命题:(1)、“等于同一个角的两个角相等”与“如果两个角都等于同一个角,那么这两个角相等”;(2)、“对顶角相等”与“如果两个角相等,那么这两个角是对顶角”;(3)、“同位角相等,两直线平行”与“同位角不相等,两直线不平行”.20. 写出下列命题的逆命题,并判断原命题与逆命题的真假.(1)、如果a>0,那么a 2 > 0 ;(2)、锐角与钝角之和等于平角;(3)、平行于同一条直线的两直线平行;(4)、两直线平行,同位角的角平分线也互相平行.21.(1)、如图,AB//CD , AB、DE相交于点G , ∠B=∠D .

在下列括号内填写推理的依据:
∵ AB // CD(已知),
∴ ∠EGA = ∠D(),
又∵ ∠B = ∠D (已知),
∴ ∠EGA = ∠B(),
∴ DE // BF ().
(2)、上述推理中,应用了哪两个互逆的真命题?22.(1)、把下面的证明补充完整: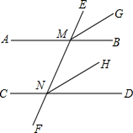
如图,已知直线EF分别交直线AB、CD于点M、N,AB∥CD,MG平分∠EMB,NH平分∠END.求证:MG∥NH
证明:∵AB∥CD(已知)
∴∠EMB=∠END( )
∵MG平分∠EMB,NH平分∠END(已知),
∴∠EMG= ∠EMB,∠ENH= ∠END( ),
∴ (等量代换)
∴MG∥NH( ).
(2)、你在第(1)小题的证明过程中,应用了哪两个互逆的真命题?请直接写出这一对互逆的真命题.