初中数学苏科版七年级下册12.2 证明 同步训练
试卷更新日期:2021-05-05 类型:同步测试
一、单选题
-
1. 下列运用等式性质进行的变形中,正确的是( )A、若a=b,则ac=bc B、若x=y,则5﹣x=5+y C、若2x=3,则x= D、若a=b,则 =2. 如图,下列判断正确的是( )
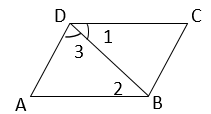 A、若∠1=∠2,则AD∥BC B、若∠1=∠2,则AB∥CD C、若∠A=∠3,则AD∥BC D、若∠3+∠ADC=180° ,则AB∥CD3. 如图,在 中, 是 延长线上点, , ,则 等于( )
A、若∠1=∠2,则AD∥BC B、若∠1=∠2,则AB∥CD C、若∠A=∠3,则AD∥BC D、若∠3+∠ADC=180° ,则AB∥CD3. 如图,在 中, 是 延长线上点, , ,则 等于( )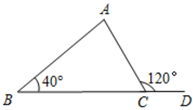 A、50° B、60° C、70° D、80°4. 如图,点 在 的延长线上,下列条件不能判断 的是( )
A、50° B、60° C、70° D、80°4. 如图,点 在 的延长线上,下列条件不能判断 的是( ) A、 B、 C、∠5=∠B D、5. 如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )
A、 B、 C、∠5=∠B D、5. 如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )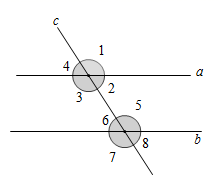 A、∠3=∠5 B、∠4=∠7 C、∠2+∠3=180° D、∠1=∠36. 如图,已知直线 , , ,则 等于( )
A、∠3=∠5 B、∠4=∠7 C、∠2+∠3=180° D、∠1=∠36. 如图,已知直线 , , ,则 等于( )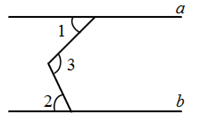 A、110° B、100° C、130° D、120°7. 如图,AB和CD相交于点O,则下列结论正确的是( )
A、110° B、100° C、130° D、120°7. 如图,AB和CD相交于点O,则下列结论正确的是( ) A、∠1=∠2 B、∠2=∠3 C、∠3=∠4 D、∠1=∠58. 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出 的是( )
A、∠1=∠2 B、∠2=∠3 C、∠3=∠4 D、∠1=∠58. 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出 的是( ) A、①② B、①③ C、②③ D、②④9. 如图,下列推理错误的是( )
A、①② B、①③ C、②③ D、②④9. 如图,下列推理错误的是( )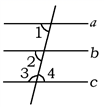 A、∵ , B、∵ C、 D、∵10. 如图,已知 .则结论① ;② 平分 ;③ ;④ .正确的是( )
A、∵ , B、∵ C、 D、∵10. 如图,已知 .则结论① ;② 平分 ;③ ;④ .正确的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
11. 已知AD//BE ,∠1=∠2,试说明∠A=∠E的理由.

解:因为∠1=∠2(已知),
所以// ,
所以∠E+∠=180°
因为AD//BE(已知),
所以∠A+∠=180°
所以∠A=∠E
12. 如图, , 相交于点 , , ,过 作 ,垂足为 .求证: .
证明:∵ ,
又 ()
∴
∴ ()
∴ ()
∵
∴ ()
∴
∴
13. 如图,已知CD⊥DA,DA⊥AB,∠1=∠4.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵()
∴∠CDA=90°,∠DAB=90°().
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴(),
∴DF∥AE().
14. 推理填空,如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.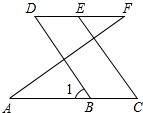
解:∵∠A=∠F(),
∴AC∥DF(),
∴∠D=∠1(),
又∵∠C=∠D(),
∴∠1=∠C(),
∴BD∥CE().
15. 已知:如图,在△ 中, 于点D,E是 上一点,且 .求证: .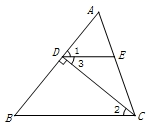
请在括号内填写出证明依据.
证明:∵ (已知)
∴ ()
∵ ()
∴ ()
∴ ∥ ()
∴ ()
16. 填写推理理由,将过程补充完整:如图, , 试说明
解: ,
(),
,
(等量代换),
,
,即 ,
(等量代换),
().
 17. 补全解答过程:
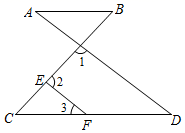
17. 补全解答过程:如图,∠1+∠2=180°,∠3=∠A .
求证:∠B=∠C .
证明:∵∠1+∠2=180°,
∴(同旁内角互补,两直线平行).
∴∠3=∠D().
又∵∠3=∠A ,
∴ .
∴AB∥CD().
∴∠B=∠C().
 18. 完成下面的证明:(1)、已知:如图,AB∥CD
18. 完成下面的证明:(1)、已知:如图,AB∥CD求证:∠1+∠3 = 180°

证明:∵ AB∥CD(已知),
∴ ∠1+∠2 = 180°()
又∵ ∠2 = ∠3()
∴ ∠1+∠3=180°()
(2)、已知:如图,AM∥EF , ∠1 = ∠B .求证:∠2 = ∠C .
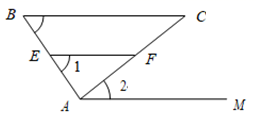
证明:∵ ∠1 = ∠B(已知),
∴ EF∥BC()
∵ AM∥EF(已知),
∴ AM∥BC()
∴ ∠2 = ∠C()
三、解答题
-
19. 如图,已知∠1=∠2,∠C=∠F.请指出∠A与∠D 的数量关系,并说明理由.
 20. 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D. 试说明:AC∥DF.
20. 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D. 试说明:AC∥DF. 21. 已知:如图,∠1=∠2,∠3=∠E,证明:∠A=∠EBC.
21. 已知:如图,∠1=∠2,∠3=∠E,证明:∠A=∠EBC.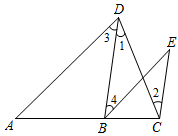 22. 完善下列证明过程,已知:如图,已知∠DAF=∠F,∠B=∠D.证明:AB∥DC
22. 完善下列证明过程,已知:如图,已知∠DAF=∠F,∠B=∠D.证明:AB∥DC
证明:∵∠DAF=∠F ( ▲ )
∴ ▲ ∥ ▲ ( ▲ )
∴∠D=∠DCF ( ▲ )
∵∠B=∠D( ▲ )
∴∠ ▲ =∠DCF (等量代换)
∴AB∥DC ( ▲ )
23. 已知:如图,在△ABC中CD交AB边于点D,直线DE平分 且与直线BE相交于点E, , .
求证:
证明:理由如下:
平分 (已知)
(已知)
(等量代换)
又 (已知)
(等量代换)
24. 如图,已知 ,∠B=∠D,AE交BC的延长线于点E. (1)、求证: ;(2)、若∠1=∠2=60°,∠BAC=2∠EAC,求∠DCE的度数.25. 已知:直线 分别与直线 , 交于点 , . 平分 , 平分 ,并且 .
(1)、求证: ;(2)、若∠1=∠2=60°,∠BAC=2∠EAC,求∠DCE的度数.25. 已知:直线 分别与直线 , 交于点 , . 平分 , 平分 ,并且 . (1)、如图1,求证: ;(2)、如图2, ,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为 .26. 如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)、如图1,求证: ;(2)、如图2, ,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为 .26. 如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F. (1)、当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为.(2)、当△PMN所放位置如图②所示时,PN交CD于点H.请猜想∠PFD与∠AEM的数量关系并证明.(3)、在(2)的条件下,若MN与CD交于点O,且∠DON=20°,∠PEB=15°,求∠N的度数.
(1)、当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为.(2)、当△PMN所放位置如图②所示时,PN交CD于点H.请猜想∠PFD与∠AEM的数量关系并证明.(3)、在(2)的条件下,若MN与CD交于点O,且∠DON=20°,∠PEB=15°,求∠N的度数.