初中数学苏科版七年级下册11.3 不等式的性质同步训练

试卷更新日期：2021-05-05 类型：同步测试

进入出卷网下载

一、单选题

1. 若m﹣n＞0，则下列各式中一定正确的是（）

A、m＞n B、mn＞0 C、 $\frac{m}{n} < 0$ D、m+n>0

查看试题解析
2. 若a＞b，则下列不等式中成立的是（）

A、ac＞bc B、ac²＞bc² C、|a|＞|b| D、ac²≥bc²

查看试题解析
3. 下列变形正确的是（　　）

A、若m＞n，则mc＞nc B、若m＞n，则mc²＞nc² C、若m＞b，b＜c，则m＞c D、若m+c²＞n+c² ，则m＞n

查看试题解析
4. 若 $ab < 0$ ，且 $a < b$ ，下列解不等式正确的是（）

A、由 $ax < b$ ，得 $x < \frac{b}{a}$ B、由 $(b - a) x < 2$ ，得 $x < \frac{2}{b - a}$ C、由 $bx < a$ ，得 $x > \frac{a}{b}$ D、由 $(a - b) x > 2$ ，得 $x > \frac{2}{a - b}$

查看试题解析
5. 如果m<n<0，那么下列式子中错误的是（）

A、m－9<n－9 B、－m>－n C、 $\frac{1}{m}$ < $\frac{1}{n}$ D、 $\frac{m}{n}$ >1

查看试题解析
6. 不论 $x$ 为何值，下列不等式恒成立的是（）

A、 $x + 1000 \geq 0$ B、 $x - 1000 \leq 0$ C、 $- {(x + 1000)}^{2} + 2 \leq 0$ D、 $- {(x + 1000)}^{2} + 2 \leq 2$

查看试题解析
7. 若代数式 $\frac{2 x + 3}{7}$ 的值是非负数，则x的取值范围是（）

A、x≥ $\frac{3}{2}$ B、x≥－ $\frac{3}{2}$ C、x> $\frac{3}{2}$ D、x>－ $\frac{3}{2}$

查看试题解析
8. 如果（a+1）x＜a+1的解集是x＞1，那么a的取值范围是（）

A、a＜0 B、a＜﹣1 C、a＞﹣1 D、a是任意有理数

查看试题解析
9. 以下说法中正确的是（）

A、若 $a > | b |$ ，则 $a^{2} > b^{2}$ B、若 $a > b$ ，则 $\frac{1}{a} < \frac{1}{b}$ C、若 $a > b$ 则 $a c^{2} > b c^{2}$ D、若 $a > b$ ， $c > d$ ，则 $a - c > b - d$

查看试题解析
10. a，b，c在数轴上的对应点的位置如图所示，下列式子：①b＋c＞0；②a＋b＞a＋c；③bc＞ac；④ab＞ac.其中正确的有（）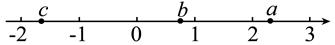

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 指出下面变形根据的是不等式的哪一条基本性质：（填阿拉伯数字）

(1)、由 $a + 3 > 0$ ，得 $a > - 3$ ；根据不等式的基本性质；

(2)、由 $- 2 a < 1$ ，得 $a > - \frac{1}{2}$ ；根据不等式得基本性质；

查看试题解析
12. 若 $m < n$ ，则2-3m2-3n(填“ $>$ ”或“ $<$ ”)．

查看试题解析
13. 当x＜a＜0时，x²ax（填＞，＜，=）

查看试题解析
14. 若不等式（4-k）x＞-1的解集为x $< \frac{1}{k - 4}$ ，则k的取值范围是．

查看试题解析
15. 若关于x的不等式 $a x - b > 0$ 的解集为 $x < \frac{1}{3}$ ，则关于 $x$ 的不等式 $(a + b) x > a - b$ 的解集为．

查看试题解析
16. 利用不等式的性质填“>”或“<”.

(1)、若a>b,则2a+12b+1；

(2)、若-1.25y<-10,则y8；

(3)、若a<b,且c<0,则ac+cbc+c；

(4)、若a>0,b<0,c<0,则(a-b)c0.

查看试题解析

三、解答题

17. 利用不等式的基本性质，将下列不等式化为“x>a”或“x<a”的形式：

(1)、x＋2>7.

(2)、3x<－12.

(3)、－7x>－14.

(4)、 $\frac{1}{3}$ x<2.

查看试题解析
18. 利用不等式的性质填“>”或“<”.

(1)、若a>b，则2a+12b+1；

(2)、若-1.25y<-10，则y8；

(3)、若a<b，且c<0，则ac+cbc+c；

(4)、若a>0，b<0，c<0，则(a-b)c0.

查看试题解析
19. 说出下列不等式的变形是根据不等式的哪一条性质：

(1)、由3＋x≤5，得x≤2；

(2)、由3x≥2x－4，得x≥－4.

查看试题解析
20.

(1)、若x>y ，请比较2－3x 与 2－3y 的大小，并说明理由．

(2)、若x>y，请比较(a－3)x与(a－3)y的大小．

查看试题解析
21. 如图，在数轴上，点A、B分别表示数1、-2x+3

(1)、求x的取值范围；

(2)、试判断数轴上表示数-x+2的点落在“点A的左边”．

查看试题解析

初中数学苏科版七年级下册11.3 不等式的性质 同步训练

一、单选题

二、填空题

三、解答题

初中数学苏科版七年级下册11.3 不等式的性质同步训练