初中数学浙教版八年级下册第五章 特殊平行四边形 章末检测（提高篇）
试卷更新日期：2021-05-04 类型：单元试卷
一、单选题
-
1. 如图，在四边形 中， 平分 ， ， ， ， ，则四边形 的周长是（ ）.
A、18 B、20 C、22 D、242. 在如图所示的正方形网格中，已知小正方形的边长为1，△ABC与△DEF的顶点均为格点，边AC、DF交于点G．下面有四个结论：①△ABC≌△DEF；②图中阴影部分(即△ABC与△DEF重叠部分)的面积为1.5；③△DCG为等边三角形；④AG=DG．其中结论正确的个数为（ ）
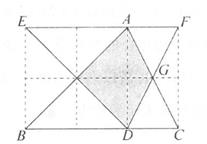A、1个 B、2个 C、3个 D、4个3. 如图，在菱形ABCD中，AB=AC=1，点E、F分别为边AB、BC上的点，且AE=BF，连接CE、AF交于点H，连接DH交AC于点O，则下列结论：①△ABF≌△CAE；②∠FHC=∠B；③△ADO≌△ACH；④ ；其中正确的结论个数是（ ）
A、1个 B、2个 C、3个 D、4个4. 在数学课拓展课上，小明发现：若一条直线经过平行四边形对角线的交点，则这条直线平分该平行四边形的面积．如图是由5个边长是1，且一个内角是60°的小菱形拼成的图形，P是其中4个小菱形的公共顶点，小新在小明的启发下，将该图形沿着过点P的某条直线剪一刀，把它剪成了面积相等的两部分，则剪痕的长度是（ ）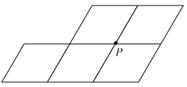
A、2 B、3 C、 D、5. 如图，平行四边形ABCD对角线AC、BD交于点O，∠ADB=20°，∠ACB=50°，过点O的直线交AD于点E，交BC于点F当点E从点A向点D移动过程中（点E与点A、点D不重合），四边形AFCE的形状变化依次是（ ）
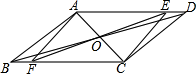A、平行四边形→矩形→平行四边形→菱形→平行四边形 B、平行四边形→矩形→平行四边形→正方形→平行四边形 C、平行四边形→菱形→平行四边形→矩形→平行四边形 D、平行四边形→矩形→菱形→正方形→平行四边形6. 在菱形ABCD中，M ， N ， P ， Q分别为边AB ， BC ， CD ， DA上的一点(不与端点重合)，对于任意的菱形ABCD ， 下面四个结论中：①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形
正确的结论的个数是（ ）
A、1个 B、2个 C、3个 D、4个7. 矩形各内角的平分线能围成一个（ ）A、矩形 B、菱形 C、等腰梯形 D、正方形8. 如图为某城市部分街道示意图，四边形ABCD为正方形，点G在对角线BD上，GE⊥CD，GF⊥BC，AD=1500m，小敏行走的路线为B→A→G→E，小聪行走的路线为B→A→D→E→F，若小敏行走的路程为3100m，则小聪行走的路程为（ ）m．
A、3100 B、4600 C、3000 D、36009. 如图，矩形ABCD中，对角线AC，BD交于点O，E，F分别是边BC，AD的中点，AB=2，BC=4，一动点P从点B出发，沿着B﹣A﹣D﹣C在矩形的边上运动，运动到点C停止，点M为图1中某一定点，设点P运动的路程为x，△BPM的面积为y，表示y与x的函数关系的图象大致如图2所示．则点M的位置可能是图1中的（ ）
A、点C B、点O C、点E D、点F10. 七巧板是我国祖先的一项卓越创造，流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板，如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形，则这两个图形中，中国七巧板和日本七巧板能拼成的个数分别是（ ）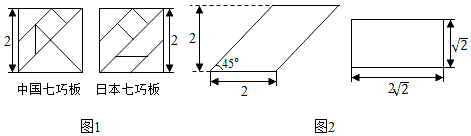
A、1和1 B、1和2 C、2和1 D、2和2二、填空题
-
11. 如图，在矩形ABCD中，∠ACB=30°，BC=2 ，点E是边BC上一动点（点E不与B，C重合），连接AE，AE的中垂线FG分别交AE于点F，交AC于点G，连接DG，GE．设AG=a，则点G到BC边的距离为（用含a的代数式表示）， ADG的面积的最小值为 ．
12. 如图，在矩形ABCD中， AB＝3，AD＝10，点E在AD上且DE＝2.点G为AE的中点，点P为BC边上的一个动点，F为EP的中点，则GF＋EF的最小值为.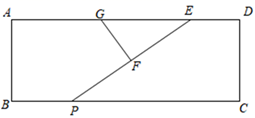
13. 如图，两张等宽的纸条交叉叠放在一起，若重叠都分构成的四边形ABCD中，AB=3，BD=4．则AC的长为 ．
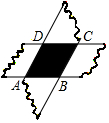14. 如图，A，B两点的坐标分别为（6，0)，(0，6)，点P从点A出发，沿AB方向以每秒 个单位的速度向终点B运动；同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动，将△PQO沿BO翻折，点P的对应点为点C，若四边形QPOC为菱形，则点C的坐标为.
15. 如图，正方形 面积为1，延长 至点G，使得 ，以 为边在正方形另一侧作菱形 ，其中 ，依次延长 类似以上操作再作三个形状大小都相同的菱形，形成风车状图形，依次连结点 则四边形 的面积为.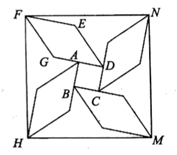
16. 如图，正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内，它们的边平行于x轴或y轴，其中点A、A1、A2在直线OM上，点C、C1、C2在直线ON上，O为坐标原点，已知点A的坐标为（3，3），正方形ABCD的边长为1.若正方形A2B2C2D2的边长为2011，则点B2的坐标为.
三、解答题
-
17. 如图，矩形ABCD中，AB=4，BC=10，E在AD上，连接BE，CE，过点A作AG∥CE，分别交BC，BE于点G，F，连接DG交CE于点H．若AE=2，求证：四边形EFGH是矩形．
18. 如图所示，矩形ABCD的对角线相交于点O，OF⊥AD于点F，OF＝2cm，AE⊥BD于点E，且BE﹕BD＝1﹕4，求AC的长.
19. 如图1，点C在线段AB上，分别以AC、BC为边在线段AB的同侧作正方形ACDE和正方形BCMN，连结AM、BD．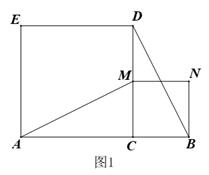
(1)、AM与BD的关系是： ．(2)、如果将正方形BCMN绕点C顺时针旋转锐角α，它不变（如图2）．（1）中所得的结论是否仍然成立？请说明理由．
(3)、在（2）的条件下，连接AB、DM，若AC＝4，BC＝2，求 的值．20. 如图，矩形 的顶点A、C分别在x轴、y轴的正半轴上，点 的坐标为（3，4），一次函数 的图象与边OC、AB分别交于点D、E，并且满足 ，M是线段DE上的一个动点
(1)、求b的值；(2)、连接OM，若 的面积与四边形 的面积之比为 ，求点M的坐标；(3)、设N是x轴上方平面内的一点，以O、D、M、N为顶点的四边形是菱形，求点N的坐标.21. 如图，等腰△ABC中，已知AC＝BC＝ ，AB＝2，作∠ACB的外角平分线CF，点E从点B沿着射线BA以每秒1个单位的速度运动，过点E作BC的平行线交CF于点F.
(1)、求证：四边形BCFE是平行四边形；(2)、当点E是边AB的中点时，连接AF，试判断四边形AECF的形状，并说明理由；(3)、设运动时间为t秒，是否存在t的值，使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形？不存在的，试说明理由；存在的，请直接写出t的值.22. 已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F ， 垂足为O ．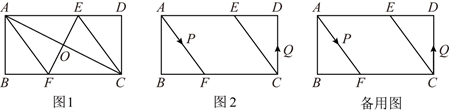
(1)、如图1，连接AF、CE，求证：四边形AFCE为菱形；(2)、如图1，求AF的长；(3)、如图2，动点P、Q分别从A、C两点同时出发，沿ΔAFB和ΔCDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止.在运动过程中，点P的速度为每秒1cm，设运动时间为t秒.若点Q的速度为每秒0.8cm，当A、P、C、Q四点为顶点的四边形是平行四边形时，求t的值．23. 如图1，已知正方形ABCD的顶点A，B分别在y轴和x轴上，边CD交x轴的正半轴于点E．
(1)、若A（0，a），且 ，求A点的坐标；(2)、在（1）的条件下，若3AO=4EO，求D点的坐标；(3)、如图2，连结AC交x轴于点F，点H是A点上方y轴上一动点，以AF、AH为边作平行四边形AFGH，使G点恰好落在AD边上，试探讨BF，HG与DG的数量关系，并证明你的结论．24. 如图，在边长为 的正方形ABCD中，作∠ACD的平分线交AD于F ， 过F作直线AC的垂线交AC于P ， 交CD的延长线于Q ， 又过P作AD的平行线与直线CF交于点E ， 连接DE ， AE ， PD ， PB ．
(1)、求AC ， DQ的长；(2)、四边形DFPE是菱形吗？为什么？(3)、探究线段DQ ， DP ， EF之间的数量关系，并证明探究结论；(4)、探究线段PB与AE之间的数量关系与位置关系，并证明探究结论．