初中数学浙教版八年级下册第五章 特殊平行四边形 章末检测(基础篇)
试卷更新日期:2021-05-04 类型:单元试卷
一、单选题
-
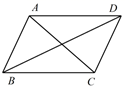
1. 在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( )A、BC=CD B、AB=CD C、∠D=90° D、AD=BC2. 菱形具有而矩形不具有的性质是( )A、两组对边分别平行 B、对角线互相垂直 C、对角线互相平分 D、两组对角分别相等3. 如图,已知四边形 ABCD 是平行四边形,下列结论中不正确的是( )
 A、当 AB=BC 时,它是菱形 B、当 AC⊥BD 时,它是菱形 C、当 ∠ABC=90° 时,它是矩形 D、当 AC=BD 时,它是正方形4. 下列说法中,错误的是( )A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直平分 C、矩形的对角线互相垂直 D、正方形的对角线相等5. 如图,已知点P为长方形 内一点(不含边界),设 ,若 ,则( )
A、当 AB=BC 时,它是菱形 B、当 AC⊥BD 时,它是菱形 C、当 ∠ABC=90° 时,它是矩形 D、当 AC=BD 时,它是正方形4. 下列说法中,错误的是( )A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直平分 C、矩形的对角线互相垂直 D、正方形的对角线相等5. 如图,已知点P为长方形 内一点(不含边界),设 ,若 ,则( )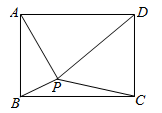 A、 B、 C、 D、6. 如图,四边形 是长方形,点 是 长线上一点, 是 上一点,并且 , .若 ,则 的度数是( )
A、 B、 C、 D、6. 如图,四边形 是长方形,点 是 长线上一点, 是 上一点,并且 , .若 ,则 的度数是( ) A、 B、 C、30° D、7. 如图,在 中, , 于点 , 是 的外角的平分线, 交 于点 ,则四边形 的形状是( )
A、 B、 C、30° D、7. 如图,在 中, , 于点 , 是 的外角的平分线, 交 于点 ,则四边形 的形状是( )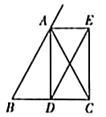 A、平行四边形 B、矩形 C、菱形 D、正方形8. 如图,四边形 OABC 是矩形,A(2,1),B(0,5),点 C 在第二象限,则点 C 的坐标是( )
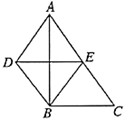
A、平行四边形 B、矩形 C、菱形 D、正方形8. 如图,四边形 OABC 是矩形,A(2,1),B(0,5),点 C 在第二象限,则点 C 的坐标是( )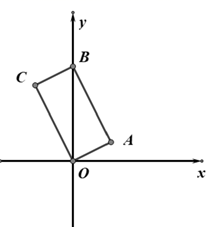 A、(1,3) B、(﹣1,2) C、(﹣2,﹣3) D、(﹣2,4)9. 在平面直角坐标系中,菱形ABCD的顶点的坐标A,B,C分别为(﹣2,0),(0,1),(2,0),则顶点D的坐标为( )A、(0,﹣1) B、(﹣2,1) C、(2,1) D、(0,﹣2)10. 七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是用右图所示的七巧板拼成的,则不能用七巧板拼成的那幅图是( )
A、(1,3) B、(﹣1,2) C、(﹣2,﹣3) D、(﹣2,4)9. 在平面直角坐标系中,菱形ABCD的顶点的坐标A,B,C分别为(﹣2,0),(0,1),(2,0),则顶点D的坐标为( )A、(0,﹣1) B、(﹣2,1) C、(2,1) D、(0,﹣2)10. 七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是用右图所示的七巧板拼成的,则不能用七巧板拼成的那幅图是( ) A、金字塔
A、金字塔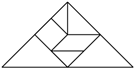 B、拱桥
B、拱桥 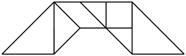 C、房屋
C、房屋 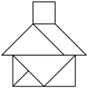 D、金鱼
D、金鱼 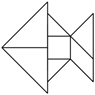
二、填空题
-
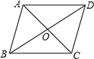
11. 杨师傅要做一个长方形的桌面,做好后量得长为2m,宽为1.5m,对角线为2.15m,则这个桌面.(填“合格”或“不合格”).12. 如图,四边形 的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是 .
 13. 菱形的面积是16,一条对角线长为4,则另一条对角线的长为.14. 如图,菱形ABCD中,AC=8,BD=6,则该菱形ABCD的周长为.
13. 菱形的面积是16,一条对角线长为4,则另一条对角线的长为.14. 如图,菱形ABCD中,AC=8,BD=6,则该菱形ABCD的周长为.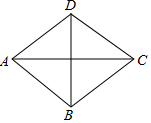 15. 如图,P是正方形ABCD内的一点,PA=PB=10,并且P点到CD的距离也等于10,则正方形面积是
15. 如图,P是正方形ABCD内的一点,PA=PB=10,并且P点到CD的距离也等于10,则正方形面积是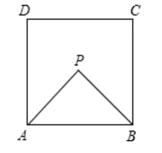 16. 正方形 的对角线长为 ,面积为.
16. 正方形 的对角线长为 ,面积为.三、解答题
-
17. 如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?
 18. 如图,△ABC中,AB=AC,AD是 的平分线,E为AD延长线上一点,CF//BE且交AD于F,连接BF、CE.
18. 如图,△ABC中,AB=AC,AD是 的平分线,E为AD延长线上一点,CF//BE且交AD于F,连接BF、CE.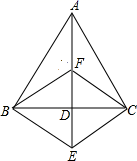
求证:四边形BECF是菱形.
19. 如图,在正方形ABCD中,E是AD的中点,F是 AB上一点,且AF= AB.求证:CE⊥EF.
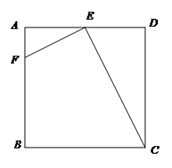 20. 如图,16个形状大小完全相同的菱形组成网格 ,菱形的顶点称为格点.
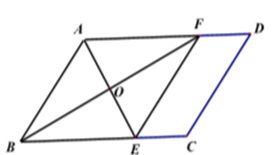
20. 如图,16个形状大小完全相同的菱形组成网格 ,菱形的顶点称为格点.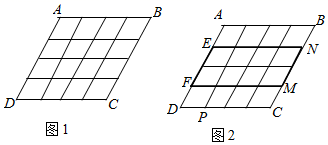 (1)、在图1中画出矩形 ,使得 , , , 分别落在 , , , 边(包含端点)的格点上;(2)、如图2,已知点 , , , , 均在格点上,请在网格中(包含边界)找一格点 ,连结 ,使得直线 平分 的面积.21. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)、在图1中画出矩形 ,使得 , , , 分别落在 , , , 边(包含端点)的格点上;(2)、如图2,已知点 , , , , 均在格点上,请在网格中(包含边界)找一格点 ,连结 ,使得直线 平分 的面积.21. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.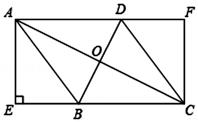 (1)、求证:四边形AECF是矩形;(2)、连接OE,若AD=5,BE=3,求线段OE的长.
(1)、求证:四边形AECF是矩形;(2)、连接OE,若AD=5,BE=3,求线段OE的长.