初中数学浙教版八年级下册5.3.2正方形的性质与判定 同步练习
试卷更新日期：2021-05-04 类型：同步测试
一、单选题
-
1. 如图，正方形ABCD的边长为4，点4的坐标为（-1，1），AB平行于x轴，则点C的坐标为（ ）
A、（3，1） B、（-1，1） C、（3，5） D、（-1，5）2. 下列说法正确的个数是（ ）①对角线互相垂直或有一组邻边相等的矩形是正方形；②对角线相等或有一个角是直角的菱形是正方形；③对角线互相垂直且相等的平行四边形是正方形；④对角线互相垂直平分且相等的四边形是正方形.
A、1个 B、2个 C、3个 D、4个3. 正方形ABCD中，对角线AC、BD交于点O，则∠CBO等于（ ）A、30° B、45° C、60° D、75°4. 如图所示，正方形ABCD的边长为1，AB在x轴的正半轴上，以A（1，0）为圆心，AC为半径作圆交x轴负半轴于点P，则点P的横坐标是（ ）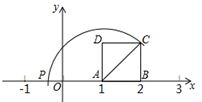
A、 B、 C、 D、5. 如图所示，正方形ABCD的边长为4，点M在边DC上，且DM＝1，点N是边AC上一动点，则线段DN+MN的最小值为（ ）
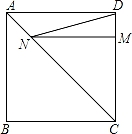A、4 B、4 C、2 D、56. 小明用四根长度相同的木条首尾相接制作了能够活动的学具，他先活动学具成为图1所示，并测得∠ABC＝60°，接着活动学具成为图2所示，并测得∠ABC＝90°，若图2对角线BD＝20cm，则图1中对角线BD的长为（ ）
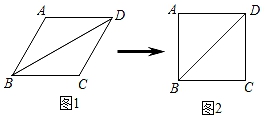A、10cm B、10 cm C、10 cm D、10 cm7. 如图①、图②，在给定的一张矩形纸片上作一个正方形，甲、乙两人的作法如下：甲：以点A为圆心，AD长为半径画弧，交AB于点E，以点D为圆心，AD长为半径画弧，交CD于点F，连接EF，则四边形AEFD即为所求；
乙：作∠DAB的平分线，交CD于点M，同理作∠ADC的平分线，交AB于点N，连接MN，则四边形ADMN即为所求．
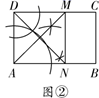
对于以上两种作法，可以做出的判定是（ ）
A、甲正确，乙不正确 B、甲、乙正确 C、乙正确，甲不正确 D、甲、乙均不正确8. 如图，在四边形ABCD中，点O是对角线的交点，能判定这个四边形是正方形的是（ ）
A、AC=BD，AB∥CB，AD∥BC B、AD∥BC，∠BAD =∠BCD C、AO=CO，BO=DO，AB=BC D、AO=BO=CO=DO，AC⊥BD9. 如图，在△ABC中，∠ACB＝90°，AC＝8，BC＝7，以斜边AB为边向外作正方形ABDE ， 连接CE ， 则CE的长为（ ）
A、14 B、15 C、16 D、1710. 如图所示中的 的正方形网格中， （ ）
A、 B、 C、 D、二、填空题
-
11. 正方形的对角线长为2，则正方形的边长为cm.面积为cm2.12. 如图，BD是正方形ABCD的对角线，点E在CD上，若CE=3，△ABE的面积为8，则△DBE的周长为。
13. 如图，已知P是正方形ABCD对角线BD上一点，且BP = BC，则∠DCP度数是 ．
14. 如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与点B，C重合），过点C作CN⊥DM交AB于点N，连结OM、ON，MN．下列五个结论：①△CNB≌△DMC；②ON＝OM；③ON⊥OM；④若AB＝2，则S△OMN的最小值是1；⑤AN2+CM2＝MN2 ． 其中正确结论是；（只填序号）
三、解答题
-
15. 正方形的边长为2，建立适当的直角坐标系，使它的一个顶点的坐标为（ ，0），并写出另外三个顶点的坐标.16. 如图，在正方形ABCD中，E，F分别BC，CD边上的一点，且BE＝2EC，FC＝ DC，连接AE，AF，EF，求证：△AEF是直角三角形.
17. 如图（1），正方形 的对角线 相交于点 是 上一点，连接 过点A作 垂足为 与 相交于点F.
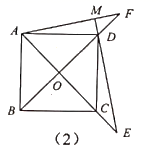(1)、直接写出 与 的数量关系；(2)、如图（2）若点E在 的延长线上， 于点 交 的延长线于点F，其他条件不变.试探究 与 的数量关系，并说明理由.18. 如图，在Rt ABC中，∠ACB＝90°．过点C的直线m∥AB，D为AB边上一点，过点D作DE⊥BC交直线m于点E，垂足为点F，连结CD、BE．
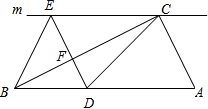(1)、求证：CE＝AD(2)、当点D是AB中点时，四边形BECD是什么特殊四边形？说明你的理由；(3)、若点D是AB中点，当四边形BECD是正方形时，则∠A大小满足什么条件？19. 已知：如图，平行四边形ABCD中，E是BC的延长线上一点，CE＝CB，AE交CD 于点O．
(1)、求证：OC＝OD；(2)、连接AC、DE，当∠B＝∠AEB时，判断四边形ACED的形状，并说明理由；(3)、在（2） 条件下，∠B＝°时，四边形ACED是正方形．