初中数学浙教版八年级下册5.3.1正方形的判定 同步练习

试卷更新日期：2021-05-04 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 要使矩形ABCD为正方形，需要添加的条件是（　　）
    A、AB=BC B、AD=BC C、AB=CD D、AC=BD

    查看试题解析

  • 2. 已知平行四边形 ABCD 中， ∠A=∠B=∠C=90∘ ，如果添加一个条件，使得该四边形成为正方形，那么所添加的这个条件可以是（    ）
    A、∠D=90∘ B、AB=CD C、AB=BC D、AC=BD

    查看试题解析

  • 3. 已知在四边形 ABCD 中， ∠A=∠B=∠C=90° ，下列可以判定四边形是正方形的是（    ）
    A、∠D=90° B、AB=CD C、AC=BD D、BC=CD

    查看试题解析

  • 4. 如图，已知线段 AB ，按下列步骤作图：分别以 A 、 B 为圆心，大于 12AB 长为半径画弧，两弧相交于点 M 、 N ，作直线 MN ，交 AB 于点 O ，分别连接 MA 、 MB 、 NA 、 NB ，如果四边形 MANB 是正方形，需要添加的条件是（    ）

    A、AO=MO B、MA//NB C、MA=NB D、AB 平分 ∠MAN

    查看试题解析

  • 5. 如图，在矩形ABCD内有一点F，FB与FC分别平分∠ABC和∠BCD，点E为矩形ABCD外一点，连接BE，CE．现添加下列条件：①EB∥CF，CE∥BF；②BE=CE，BE=BF；③BE∥CF，CE⊥BE；④BE=CE，CE∥BF，其中能判定四边形BECF是正方形的共有（   ）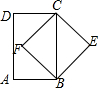

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 6. 已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（    ）

    A、选①② B、选选①③ C、选②③ D、选②④

    查看试题解析

  • 7. 将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当 ∠B=90° 时，如图1，测得AC=2，当 ∠B=60° 时，如图2，则AC的值为（   ）

     

    A、22 B、6 C、2 D、2

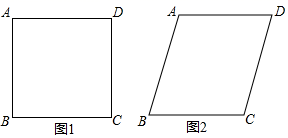    查看试题解析

  • 8. 在矩形ABCD中，E，P，G，H分别是边AB，BC，CD，DA上的点(不与端点重合)，对于任意矩形ABCD，下面四个结论中正确的是（   ）

    ①存在无数个四边形EFGH是平行四边形.②存在无数个四边形EFGH是矩形.③存在且仅有一个四边形EFGH是菱形.④除非矩形ABCD为正方形，否则不存在四边形EFGH是正方形.

    A、①② B、①②③ C、①②④ D、①③④

    查看试题解析

  • 9. 下列命题中，真命题是（    ）
    A、有一组边相等的平行四边形是菱形； B、有一个角是直角的平行四边形是正方形； C、有一个角为直角的菱形是正方形； D、两条对角线相等的四边形是矩形．

    查看试题解析

  • 10. 如图，AC、BD是四边形ABCD的对角线，若E、F、G、H分别是BD、BC、AC、AD的中点，顺次连接E、F、G、H四点，得到四边形EFGH，则下列结论不正确的是（　　）

    A、四边形EFGH一定是平行四边形 B、当AB=CD时，四边形EFGH是菱形 C、当AC⊥BD时，四边形EFGH是矩形 D、四边形EFGH可能是正方形

    查看试题解析

二、填空题

  • 11. 如图，在△ABC中，点D，E，F分别是△ABC的边AB，BC，AC上的点，且DE∥AC，EF∥AB，要使四边形ADEF是正方形，还需添加条件：.

    查看试题解析

  • 12. 如图在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，请你添加一个条件 ， 使四边形BECF是正方形.

    查看试题解析

  • 13. 如图，在一块木板上钉上9颗钉子，每行和每列的距离都一样，以钉子为顶点拉上橡皮筋，组成一个正方形，这样的正方形一共有个.

    查看试题解析

  • 14. 如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点，当AB：AD=时，四边形MENF是正方形．

    查看试题解析

三、解答题

  • 15. 如图，将 RtΔADF 绕着点A顺时针旋转 90° 得到 RtΔABE ，射线 EB 与 DF 相交于点C， ∠D=90° ，求证：四边形 ABCD 为正方形．

    查看试题解析

  • 16. 如图，在平面直角坐标系中，四边形ABCD的顶点坐标分别是A（-2，0）、B(0，-2)、C（2，0）、D（0，2），求证：四边形ABCD是正方形.

    查看试题解析

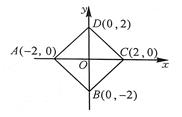  • 17. 如图，在△ABC中，点D是BC边的中点，点E是AD的中点，过A点作AF∥BC ， 且交CE的延长线于点F ， 联结BF ．

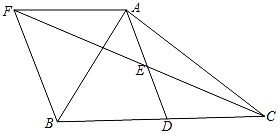    (1)、求证：四边形AFBD是平行四边形；
    (2)、当AB＝AC时，求证：四边形AFBD是矩形；
    (3)、（填空）在（2）中再增加条件 ． 则四边形AFBD是正方形．

    查看试题解析

  • 18. 如图，点E，F， G，H分别是CD，BC，AB，DA的中点.

    (1)、求证：四边形EFGH是平行四边形.
    (2)、若连接AC，BD， 则当AC，BD满足什么关系时，四边形EFGH是正方形?请说明理由.

    查看试题解析

  • 19. 如图，在△ABC中，AB=AC，E，F分别为AB，AC上的点（E，F不与A重合），且EF//BC.将△AEF沿着直线EF向下翻折，得到 △A'EF ，再展开.

    (1)、请证明四边形 AEA'F 为菱形；
    (2)、当等腰△ABC满足什么条件时，按上述方法操作，四边形 AEA'F 将变成正方形？（只写结果，不作证明）

    查看试题解析