初中数学浙教版八年级下册5.2.2菱形的判定 同步练习
试卷更新日期：2021-05-03 类型：同步测试
一、单选题
-
1. 如图，四边形ABCD沿直线l对折后重合，如果 ，则结论①AB CD；②AB=CD；③ ；④ 中正确的是（ ）
A、1个 B、2个 C、3个 D、4个2. 如图，在 中，点D在边BC上，过点D作 ， ，分别交AB，AC于E，F两点．则下列命题是假命题的是（ ）
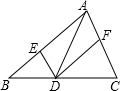A、四边形 是平行四边形 B、若 ，则四边形 是矩形 C、若 ，则四边形 是菱形 D、若 ，则四边形 是矩形3. 如图，在平行四边形ABCD中，点F是AB的中点，连接DF并延长，交CB的延长线于点E ， 连接AE ． 添加一个条件，使四边形AEBD是菱形，这个条件是（ ）
A、 B、 C、 D、DE平分4. 两张全等的矩形纸片 ABCD，AECF 按如图方式交叉叠放在一起，AB=AF，AE=BC.若 AB=1，BC=3，则图中重叠（阴影）部分的面积为（ ）.
A、2 B、 C、 D、5. 某班同学在“为抗疫英雄祈福”的主题班会课上制作象征“平安归来”的黄丝带，如图所示，丝带重叠部分形成的图形是（ ）
A、矩形 B、菱形 C、正方形 D、等腰梯形6. 如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AB＝4，BC＝3，则四边形CODE的周长是（ ）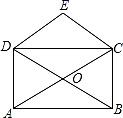
A、5 B、8 C、10 D、127. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF＝12，AB＝10，则AE的长为（ ）
A、16 B、15 C、14 D、138. 如图，在 ABCD中，DE，BF分别是∠ADC和∠ABC的平分线，添加一个条件，仍无法判断四边形BFDE为菱形的是（ ）
A、∠A=60˚ B、DE=DF C、EF⊥BD D、BD 是∠EDF的平分线9. 如图，某同学作线段AB的垂直平分线：分别以点A和点B为圆心，大于 AB的长为半径画弧，两弧相交于点C，D，则直线CD为线段AB的垂直平分线.根据这个同学的作图方法可知四边形ADBC一定是（ ）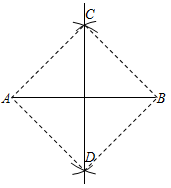
A、菱形 B、平行四边形 C、矩形 D、一般的四边形10. 已知四边形ABCD是平行四边形，下列结论错误的是（ ）A、当AB=BC时，它是菱形 B、当AC⊥BD时，它是菱形 C、当 时，它是矩形 D、当 时，它是菱形二、填空题
-
11. 如图，在▱ABCD中，以点A为圆心，以任意长为半径画圆弧，分别交边AD、AB于点M、N ， 再分别以点M、N为圆心，以大于 长为半径画圆弧，两弧交于点P ， 作射线AP交边CD于点E ， 过点E作EF∥AD交AB于点F ． 若AB=5，CE=2，则四边形ADEF的周长为 ．
12. 如图，小华剪了两条宽为3的纸条，交叉叠放在一起，且它们较小的交角为60°，则它们重叠部分的面积为.
13. 如图，在四边形ABCD中，对角线AC，BD交于点O，AC与BD互相垂直且平分，BD＝10，AC＝24，则四边形周长为 ， 面积为.
14. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=8，AB=5，则AE的长为 ．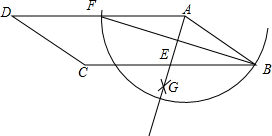
三、解答题
-
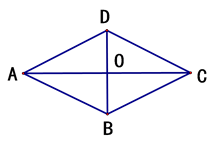
15. 如图，平行四边形ABCD的对角线交于点O，且AB=13，AC=24，BD=10．求证：四边形ABCD是菱形．
16. 已知：如图，在△ABC中，AD是∠BAC的平分线，DE∥AC，DF∥AB.求证：四边形AEDF是菱形.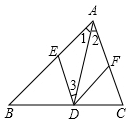
17. 老师布置了一个作业，如下：已知：如图1 的对角线 的垂直平分线 交 于点 ，交 于点 ，交 于点 ．求证：四边形 是菱形．
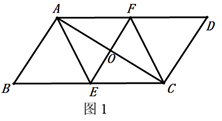
嘉琪同学写出了如图2所示的证明过程，老师说嘉琪同学的作业是错误的．请你解答下列问题：
(1)、能找出该同学错误的原因吗？请你指出来；(2)、请你给出本题的符合题意证明过程．18. 如图，在矩形ABCD中，M、N分别是AD、BC的中点，P、Q分别是BM、DN的中点．
(1)、求证：△MBA≌△NDC；(2)、四边形MPNQ是什么样的特殊四边形？不用证明．19. 如图，直线y=﹣2x+8分别交x轴，y轴于点A ， B ， 直线y x+3交y轴于点C ， 两直线相交于点D ．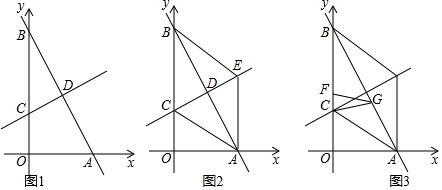
(1)、求点D的坐标；(2)、如图2，过点A作AE∥y轴交直线y x+3于点E ， 连接AC ， BE ． 求证：四边形ACBE是菱形；(3)、如图3，在（2）的条件下，点F在线段BC上，点G在线段AB上，连接CG ， FG ， 当CG=FG ， 且∠CGF=∠ABC时，求点G的坐标．