浙江省湖州市长兴县2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-04-30 类型：期中考试

进入出卷网下载

一、选择题(每小题3分，共30分)

1. 化简( $\sqrt{3}$ )²的结果是（）

A、3 B、6 C、9 D、 $\sqrt{6}$

查看试题解析
2. 下列一元二次方程中，两个根分别是-2和3的是（）

A、x²+x-6=0 B、x²-x-6=0 C、x²-5x+6=0 D、x²+5x+6=0

查看试题解析
3. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是9.2环，方差分别为 $S_{甲}^{2}$ =0.56， $S_{乙}^{2}$ =0.60， $S_{丙}^{2}$ =0.50， $S_{丁}^{2}$ =0.44，则成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{0.1}$ B、 $\sqrt{24}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{a^{2} + b^{2}}$

查看试题解析
5. 对一元二次方程 $\frac{1}{4}$ x²- $\frac{1}{2021}$ x-1=0的描述正确的是（）

A、常数项为1 B、没有实数根 C、有两个不等的实数根 D、有两个相等的实数根

查看试题解析
6. 已知样本数据3，4，6，5，7，下列说法错误的是（）

A、平均数是5 B、方差是2 C、中位数是6 D、标准差是 $\sqrt{2}$

查看试题解析
7. 在Rt△ABC中，∠C=90°，AC= $2 \sqrt{3}$ ，AB= $2 \sqrt{5}$ ，则Rt△ABC的面积为（）

A、 $2 \sqrt{6}$ B、 $2 \sqrt{10}$ C、 $2 \sqrt{15}$ D、 $4 \sqrt{2}$

查看试题解析
8. 已知4x²+4(m-2)x+m是一个关于x的完全平方式，则常数m的值是（）

A、4或9 B、1或4 C、1或9 D、1或16

查看试题解析
9. 某篮球队5名场上队员的身高(单位：cm)分别是183、187、190、200、195，现用-名身高为210cm的队员换下场上身高为195cm的队员，与换人前相比，场上队员身高的（）

A、平均数变大，方差变小 B、平均数变小，方差变大 C、平均数变大，方差变大 D、平均数变小，方差变小

查看试题解析
10. 把一个边长为40cm的正方形硬纸板的四周按如图所示的方式剪掉一些长方形，将剩余部分折成一个有盖的长方体盒子，折成的一个长方体盒子的表面积为550cm² ，则此时长方体盒子的体积为（）

A、750cm³ B、1536cm³ C、2000cm³ D、2304cm³

查看试题解析

二、填空题(每小题4分，共24分)

11. 计算： $\sqrt{2} \times \sqrt{32}$ =。

查看试题解析
12. 已知方程(x+1)(x+a)=0有一个根是x=3，则a=。

查看试题解析
13. 某次检测中，一个10人小组，其中6人的平均成绩是90分，其余4人的平均成绩是80分，那么这个10人小组的平均成绩是。

查看试题解析
14. 在平面直角坐标系中，点P( $- \sqrt{2}$ ， $\sqrt{6}$ )到原点的距离是。

查看试题解析
15. 已知一组数据从小到大排列为：-1，0，4，x，6，15，且这组数据的中位数是5，那么这组数据的众数是。

查看试题解析
16. 已知下面三个关于x的一元二次方程ax²+bx+c=1，bx²+cx+a=-3，cx²+ax+b=2恰好有一个相同的实数根，则a+b+c的值为。

查看试题解析

三、解答题(共66分)

17. 计算：

(1)、 $\sqrt{12} - \frac{1}{3} \sqrt{27} + \sqrt{48}$

(2)、 ${(\sqrt{3} - \sqrt{2})}^{2}$

查看试题解析
18. 解方程：

(1)、x²- 2x-3=0

(2)、3x²-2 $\sqrt{3}$ x=-1

查看试题解析
19. 某山区中学280名学生参加植树节活动，要求每人植3至6棵，活动结束后随机抽查了若干名学生每人的植树量，并分为四种类型，A：3棵；B：4棵；C：5棵；D：6棵，将各类的人数绘制成扇形图(如图1)和条形图(如图2)

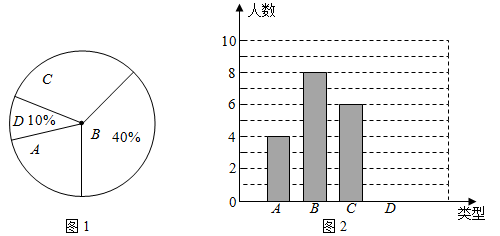
回答下列问题：

(1)、这次调查一共抽查了 ▲ 名学生的植树量；请将条形图补充完整；

(2)、被调查学生每人植树量的众数是棵，中位数是棵；

(3)、求被调查学生每人植树量的平均数，并估计这280名学生共植树多少棵？

查看试题解析
20. 如图，大坝横截面的迎水坡AD的坡比为4：3，背水坡BC的坡比是1：2，大坝高DE=20米，坝顶宽CD=10米．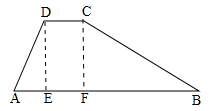

(1)、求横截面下底AB的长；

(2)、求横截面的周长。

查看试题解析
21. 高空抛物极其危险，是我们必须杜绝的行为．据研究，高空抛物下落的时间t(单位：s)和高度h(单位：m)近似满足公式t= $\sqrt{\frac{h}{5}}$ (不考虑风速的影响)．

(1)、从50m高空抛物到落地所需时间t₁是多少s，从100m高空抛物到落地所需时间t₂是多少s；

(2)、t₂是t₁的多少倍？

(3)、经过1.5s，高空抛物下落的高度是多少？

查看试题解析
22. 已知关于x的一元二次方程mx²-2x+2-m=0

(1)、证明：不论m为何值时，方程总有实数根；

(2)、当m为何整数时，方程有两个不相等的整数根。

查看试题解析
23. 某水果商场经销一种高档水果，原价每千克50元，连续两次降价后每千克32元，若每次下降的百分率相同．

(1)、求每次下降的百分率；

(2)、若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，且要尽快减少库存，那么每千克应涨价多少元？

查看试题解析
24. 如图，Rt△ABC中，∠C= 90°，BC=4 $\sqrt{3}$ cm，∠ABC=30°。点P从点B出发，沿B→A→C以每秒3cm的速度向终点C运动，同时点Q从点B出发以每秒、3cm的速度向终点C运动，其中一点到达终点即停止．设点P的运动时间为t。

(1)、当t=2秒时，求△BPQ的面积；

(2)、PQ能否与△ABC的一条边平行，如果能，求出此时t的值；如不能，说明理由；

(3)、△BPQ的面积能否为△ABC面积的三分之一？如果能，请求出的值；如果不能，请说明理由。

查看试题解析