内蒙古赤峰市2019-2020学年下学期期末高二下学期理数联考试卷(A)
试卷更新日期:2021-04-29 类型:期末考试
一、单选题
-
1. 复数 满足 ,则下列说法正确的是( )A、 为纯虚数 B、 的虚部为 C、在复平面内 对应的点位于第三象限 D、2. “直线 和直线 平行”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 根据如下样本数据:
2
3
4
5
6
4
2.5
-0.5
-2
-3
得到的回归方程为 ,则( )
A、 , B、 , C、 , D、 ,4. 的展开式中 的系数为( )A、-32 B、32 C、-8 D、85. 一个教室有6盏灯,一个开关控制1盏灯,每盏灯都能正常照明,那么这个教室能照明的方法共有( )A、64种 B、36种 C、35种 D、63种6. 将两颗骰子各掷一次,设事件 “两个点数都不相同”, “至少出现一个5点”,则概率 ( )A、 B、 C、 D、7. “数据聚清风,一捻秋意”是宋朝朱翌撰写折扇的诗句,折扇出入怀袖,扇面书画,扇骨雕琢,是文人雅士的宠物,所以又由“换袖雅物”的别号.如图是折扇的示意图,设 ,若在整个扇形区域内随机取一点.则此点取自扇面(扇环)部分的概率是( ) A、 B、 C、 D、8. 过点 的直线 将圆 分成两段圆弧,当两段圆弧中的劣弧所对的圆心角最小时,则该直线 的斜率为( )A、 B、 C、 D、9. 设抛物线 的焦点为 , 是 上的一点且在第一象限,以 为圆心,以 为半径的圆交 的准线于 , 两点,且 , , 三点共线,则点 的横坐标为( )A、8 B、12 C、10 D、610. 若函数 存在极值点,则实数 的取值范围是( )A、 B、 C、 D、11. 设常数 ,动点 分别与两个定点 , 的连线的斜率之积为定值 ,若动点 的轨迹是渐近线斜率为2的双曲线,则 ( )A、-3 B、4 C、 D、312. 若曲线 上存在两条垂直于 轴的切线,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、8. 过点 的直线 将圆 分成两段圆弧,当两段圆弧中的劣弧所对的圆心角最小时,则该直线 的斜率为( )A、 B、 C、 D、9. 设抛物线 的焦点为 , 是 上的一点且在第一象限,以 为圆心,以 为半径的圆交 的准线于 , 两点,且 , , 三点共线,则点 的横坐标为( )A、8 B、12 C、10 D、610. 若函数 存在极值点,则实数 的取值范围是( )A、 B、 C、 D、11. 设常数 ,动点 分别与两个定点 , 的连线的斜率之积为定值 ,若动点 的轨迹是渐近线斜率为2的双曲线,则 ( )A、-3 B、4 C、 D、312. 若曲线 上存在两条垂直于 轴的切线,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 若随机变量 , 满足 , ,则 .14. 一位篮球运动员投篮一次得3分概率为 ,得2分概率为 ,不得分概率为 , .若他投篮一次得分的期望为1,则 的最小值为.15. 设圆 与 轴负半轴的交点为 ,过点 且斜率为3的直线 与圆 的另一交点为 ,若 的中点 恰好落在 轴上,则 .16. 三棱锥 的各顶点都在同一球面上, 底面 ,若 , ,且 ,给出如下命题:
① 是直角三角形;②此球的表面积等于 ;
③ 平面 ;④三棱锥 的体积为 .
其中正确命题的序号为.(写出所有正确结论的序号)
三、解答题
-
17. 已知圆 的圆心在 轴的正半轴上,半径为2.且被直线 截得的弦长为 .(1)、圆 的方程;(2)、设 是直线 上动点,过点 作圆 的切线 ,切点为 ,证明:经过 , , 三点的圆必过定点,并求所有定点坐标.18. “每天锻炼一小时,健康工作五十年,幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关,从单位随机抽取30名员工进行了同卷调查,得到了如下列联表:
男性
女性
合计
爱好
6
不爱好
6
合计
16
30
(1)、请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);(2)、能否有95%的把握认为爱好运动与性别有关?(3)、若在接受调查的所有男生中按照“爱好与不爱好运动”进行分层抽样,现随机抽取8人,再从8人中抽取3人,求至少有2人“爱好运动”的概率.附:
0.05
0.010
0.005
3.841
6.635
7.879
19. 如图所示的几何体中,四边形 是正方形.四边形 是梯形 , ,平面 平面 ,且 .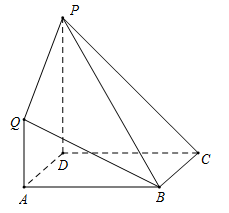 (1)、求证: 平面 ;(2)、求二面角 的大小.20. 设函数 , .
(1)、求证: 平面 ;(2)、求二面角 的大小.20. 设函数 , .(参考数值: )
(1)、证明:函数 的图象经过一个定点 ,并求出点 的切线方程;(2)、若 ,求函数 在 的值域.21. 已知椭圆 的左右焦点分别为 , , 是椭圆 上第一象限内的一点,且直线 的斜率为 .(1)、求点 的坐标;(2)、过点 作一条斜率为负数的直线 与椭圆 从左到右依次交于 , 两点.是否存在实数 ,使得 恒成立.若存在,求出 的值;若不存在,说明理由.