湘教版备考2021年中考数学二轮复习专题20一元二次方程
试卷更新日期:2021-04-28 类型:二轮复习
一、单选题
-
1. 若关于x的一元二次方程 的一个根是0,则 的值是( )A、1 B、-1 C、1或-1 D、02. 已知方程x2-6x + q = 0可以配方成(x-p)2 =7的形式,那么x2-6x +q =2可以配方成下列的( )A、(x-p)2 =9 B、(x-p)2 = 5 C、(x-p +2)2 =9 D、(x-p + 2)2 =53. 方程 的根为( )A、0或-2 B、-2 C、0 D、1或-14. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、5. 已知实数x满足(x2﹣2x+1)2+4 (x2﹣2x+1)﹣5=0,那么x2﹣2x+1的值为( )A、﹣5或1 B、﹣1或5 C、1 D、56. 若关于x的一元二次方程(m﹣1)x2+2x﹣2=0有两个不相等的实数根,则实数m的取值范围是( )A、m< B、m> C、m> 且m≠1 D、m≠17. 如果方程x2﹣x﹣2=0的两个根为α,β,那么α2+β﹣2αβ的值为( )A、7 B、6 C、﹣2 D、08. 组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请 个队参赛,则 满足的关系式为( )A、 B、 C、 D、9. 设 是方程 的两个实数根,则 的值是( )A、-6 B、-5 C、-6或-5 D、6或510. 方程x2+ax+7=0和x2﹣7x﹣a=0有一个公共根,则a的值是( )A、9 B、8 C、7 D、611. 设m是整数,关于x的方程mx2-(m-1)x+1=0有有理根,则方程的根为( )。A、 B、x=-1 C、 D、有无数个根12. 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为 ,则下面所列方程正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若关于x的三个方程x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0,(m﹣1)x2+2mx+m﹣1=0中至少有一个方程有实根,则m的取值范围是 .14. 如果关于x的一元二次方程 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.以下关于倍根方程的说法,正确的是(写出所有正确说法的序号).
①方程 是倍根方程;②若 是倍根方程,则 ;③若点 在反比例函数 的图像上,则关于 的方程 是倍根方程;④若方程 是倍根方程,且相异两点 , 都在抛物线 上,则方程 的一个根为 .
15. 设x1 , x2是一元二次方程x2+5x﹣3=0的两根,且2x1(x22+6x2﹣3)+a=4,则a= .
16. 设x,y为实数,代数式5x2+4y2﹣8xy+2x+4的最小值为 .17. 若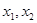 是方程 的两个实数根,且
是方程 的两个实数根,且 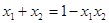 ,则 的值为.
,则 的值为.
18. 若关于x的一元二次方程(m+3)x2+5x+m2+2m-3=0有一个根是0,则m= , 另一根为。19. 若关于 的方程 有三个根,且这三个根恰好可以作为一个三角形的三条边的长,则 的取值范围是.
20. 一次棋赛,有n个女选手和9n个男选手,每位参赛者与其 个选手各对局一次,计分方式为:胜者的2分,负者得0分,平局各自得1分。比赛结束后统计发现所有参赛男选手的分数和是所有女选手的分数和的4倍,则n的所有可能值是.
三、解答题
-
21. 已知一元二次方程 的正实数根也是一元二次方程 的根,求 的值.22. 已知方程 的一个根比另一个根小4,求这两个根和 的值.23. 已知 是方程 的一个根,求方程的另一个根及c的值.24. 某旅游园区对团队入园购票规定:如团队人数不超过 人,那么这个团队需交200元入园费;若团队人数超过 人,则这个团队除了需交200元入园费外,超过部分游客还要按每人 元交入园费,下表是两个旅游团队人数和入园缴费情况:
旅游团队名称
团队人数(人)
入园费用(元)
旅游团队1
80
350
旅游团队2
45
200
根据上表的数据,求某旅游园区对团队入园购票规定的 人是多少?
四、综合题
-
25. 对于代数式ax2+bx+c,若存在实数n,当x=n时,代数式的值也等于n,则称n为这个代数式的不变值.例如:对于代数式x2 , 当x=0时,代数式等于0;当x=1时,代数式等于1,我们就称0和1都是这个代数式的不变值.在代数式存在不变值时,该代数式的最大不变值与最小不变值的差记作A. 特别地,当代数式只有一个不变值时,则A=0.(1)、代数式x2−2x的不变值是 , A=.(2)、说明代数式2x2+3没有不变值;(3)、已知代数式x2−bx+b,
①若A=0,求b的值;
②若1≤A≤2,b为整数,求所有整数b的和.
26.(1)、根据要求,解答下列问题:①方程 的解为;
②方程 的解为;
③方程 的解为;
(2)、根据以上方程特征及其解的特征,请猜想:①方程 的解为.
②关于x的方程的解为x1=1,x2=n;
(3)、请用配方法解方程 ,以验证猜想结论的正确性.27. 阅读材料:材料1:若一元二次方程ax2+bx+c=0(a≠0)的两根为x1、x2 , 则x1+x2= ,x1x2= .
材料2:已知实数m、n满足m2-m-1=0,n2-n-1=0,且m≠n,求 的值.
解:由题知m、n是方程x2-x-1=0的两个不相等的实数根,根据材料1,得m+n=1,mn=-1.
∴ .
根据上述材料解决下面的问题:
(1)、一元二次方程x2-4x-3=0的两根为x1、x2 , 则x1+x2=4,x1x2=;(2)、已知实数m,n满足 , ,且m≠n,求m2n+mn2的值;
(3)、已知实数p,q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2的值.28. 已知关于 的一元二次方程 的两个根分别为 , ,利用一元二次方程的求根公式可得: , ,利用上述结论来解答下列问题:(1)、已知 的两个根为 , ,则 , ;(2)、已知关于 的一元二次方程 有两个实数根 , ,若 ,求 的值.29. 旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多能出租一次,且每辆车的日租金是x元,发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆,已知所有观光车每天的管理费是1000元.(1)、若某日的净收入为5000元,且使游客得到实惠 , 则当天的观光车的日租金是多少元?(注:净收入=租车收入-管理费)(2)、设每日净收入为w元,请写出w与x之间的函数关系式;并求出日租金为多少时,每日净收入最大?