湘教版备考2021年中考数学二轮复习专题13直角三角形
试卷更新日期:2021-04-28 类型:二轮复习
一、单选题
-
1. 如图,AC⊥BC,垂足为C,AB=10,点A到BC的距离是8,点C到AB的距离是4.8,则点B到AC的距离是( )
 A、2.4 B、4.8 C、8 D、62. 如图,CD是直角△ABC斜边AB上的高,CB>CA,图中相等的角共有( )
A、2.4 B、4.8 C、8 D、62. 如图,CD是直角△ABC斜边AB上的高,CB>CA,图中相等的角共有( ) A、2对 B、3对 C、4对 D、5对3. 如图,已知AB⊥BD,CB⊥CD,AD=14 cm,BC=10 cm,若线段BD的长度为偶数,则线段BD的长度为( )
A、2对 B、3对 C、4对 D、5对3. 如图,已知AB⊥BD,CB⊥CD,AD=14 cm,BC=10 cm,若线段BD的长度为偶数,则线段BD的长度为( )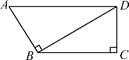 A、8 cm B、10 cm C、12 cm D、14 cm4. 直角三角形两个锐角平分线相交所成角的度数为( )A、90° B、135° C、120° D、45°或135°5. 如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )
A、8 cm B、10 cm C、12 cm D、14 cm4. 直角三角形两个锐角平分线相交所成角的度数为( )A、90° B、135° C、120° D、45°或135°5. 如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( ) A、15 海里 B、30海里 C、45海里 D、30 海里6. 下列选项不能判定 是直角三角形的是( )A、 B、 C、 D、7. 在 中, ,E是AB上一点,且 ,过E作 交AC于D,如果 ,则 等于( )
A、15 海里 B、30海里 C、45海里 D、30 海里6. 下列选项不能判定 是直角三角形的是( )A、 B、 C、 D、7. 在 中, ,E是AB上一点,且 ,过E作 交AC于D,如果 ,则 等于( )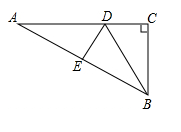 A、3cm B、4cm C、5cm D、6cm8. 下图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A,点B的位置如图所示,则点C可能的位置共有( )
A、3cm B、4cm C、5cm D、6cm8. 下图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A,点B的位置如图所示,则点C可能的位置共有( ) A、9个 B、8个 C、7个 D、6个9. 如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( )
A、9个 B、8个 C、7个 D、6个9. 如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( )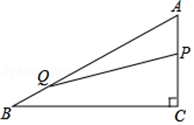 A、2s B、4s C、2s或4.5s D、2s或4s10. 如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6。其中,S1=16,S2=45,S5=11,S6=14,则S3+S4=( )
A、2s B、4s C、2s或4.5s D、2s或4s10. 如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6。其中,S1=16,S2=45,S5=11,S6=14,则S3+S4=( )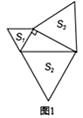
 A、86 B、64 C、54 D、4811. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角,AM=2 EF,则正方形ABCD的面积为( )
A、86 B、64 C、54 D、4811. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角,AM=2 EF,则正方形ABCD的面积为( )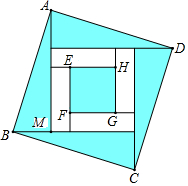 A、14S B、13S C、12S D、11S12. 如图,在 中, ,点 分别在 上,且 将 沿 所在的直线折叠得到 (点 在四边形 内),连接 则 ( )
A、14S B、13S C、12S D、11S12. 如图,在 中, ,点 分别在 上,且 将 沿 所在的直线折叠得到 (点 在四边形 内),连接 则 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,在 中, , ,BD平分 ,如果 ,那么 cm.
 14. 已知 中, , , 边上的高 ,则边 的长为 .15. 在Rt△ABC中,∠C=90°,∠A=30°,BC=5cm , 则斜边AB上的中线长是 .16. 如图,已知 ,P是射线 上一动点(即P点可在射线 上运动), .
14. 已知 中, , , 边上的高 ,则边 的长为 .15. 在Rt△ABC中,∠C=90°,∠A=30°,BC=5cm , 则斜边AB上的中线长是 .16. 如图,已知 ,P是射线 上一动点(即P点可在射线 上运动), . (1)、 时, 为直角三角形.(2)、设 ,则x满足时, 为锐角三角形.17. 若直角三角形中两个锐角的差为20°,则这两个锐角的度数分别是 .18. 如图, 中, , 点D在线段BC的延长线上, 连接AD,CD=1,BC=12,∠DAB=30°, 则AC= .
(1)、 时, 为直角三角形.(2)、设 ,则x满足时, 为锐角三角形.17. 若直角三角形中两个锐角的差为20°,则这两个锐角的度数分别是 .18. 如图, 中, , 点D在线段BC的延长线上, 连接AD,CD=1,BC=12,∠DAB=30°, 则AC= . 19. 如图所示的图形由4个等腰直角形组成,其中直角三角形(1)的腰长为1cm,则直角三角形(4)的斜边长为 .
19. 如图所示的图形由4个等腰直角形组成,其中直角三角形(1)的腰长为1cm,则直角三角形(4)的斜边长为 . 20. 如图,在Rt△ABC中,已知∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为 .
20. 如图,在Rt△ABC中,已知∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为 .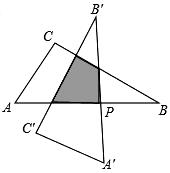
三、解答题
-
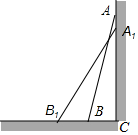
21. 如图,一根2.5米长的竹竿AB斜靠在竖直的墙AC上,这时B到墙底端为0.7米,如果竹竿的底端沿地面向外滑动0.8米,那么点A将向下移动多少米?
 22. 已知如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
22. 已知如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上. 23. 如图,两条笔直的公路 , 相交于点 , 为30°,指挥中心 设在 路段上,与 地的距离为20千米.一次行动中,王警官带队从 地出发,沿 方向行进,王警官与指挥中心均配有对讲机,两部对讲机只能在9千米之内进行通话,通过计算判断王警官在行进过程中能否与指挥中心用对讲机通话.
23. 如图,两条笔直的公路 , 相交于点 , 为30°,指挥中心 设在 路段上,与 地的距离为20千米.一次行动中,王警官带队从 地出发,沿 方向行进,王警官与指挥中心均配有对讲机,两部对讲机只能在9千米之内进行通话,通过计算判断王警官在行进过程中能否与指挥中心用对讲机通话.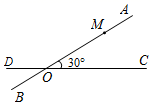 24. 三国时代东吴数学家赵爽(字君卿,约公元3世纪)在《勾股圆方图注》一书中用割补的方法构造了“弦图”(如图1,并给出了勾股定理的证明.已知,图2中涂色部分是直角边长为 ,斜边长为 的 个直角三角形,请根据图2利用割补的方法验证勾股定理.
24. 三国时代东吴数学家赵爽(字君卿,约公元3世纪)在《勾股圆方图注》一书中用割补的方法构造了“弦图”(如图1,并给出了勾股定理的证明.已知,图2中涂色部分是直角边长为 ,斜边长为 的 个直角三角形,请根据图2利用割补的方法验证勾股定理.
四、作图题
-
25. 如图,在 的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
 (1)、在图 中,画一个直角三角形,使它的三边长都是有理数;(2)、在图 中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;(3)、在图 中,画一个直角三角形,使它的三边长都是无理数.26. 如图,在6×6的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.
(1)、在图 中,画一个直角三角形,使它的三边长都是有理数;(2)、在图 中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;(3)、在图 中,画一个直角三角形,使它的三边长都是无理数.26. 如图,在6×6的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形. (1)、从点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为 ;(2)、以(1)中的AB为边的一个等腰△ABC,使点C在格点上,且三边中至少有两边的长度都是无理数.回答:符合条件的点C共有个,并在网格中画出符合条件的所有点C.
(1)、从点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为 ;(2)、以(1)中的AB为边的一个等腰△ABC,使点C在格点上,且三边中至少有两边的长度都是无理数.回答:符合条件的点C共有个,并在网格中画出符合条件的所有点C.五、综合题
-
27. 已知 ≌ , .


 (1)、将 和 按图①方式摆放,使 经过点 ,延长 交线段 于点 .试判断线段 、 、 之间的数量关系,并证明你的结论;(2)、将 和 按图②方式摆放,延 交线段 于点 .请直接写出 、 、 之间的数量关系 .(3)、将 和 按图③方式摆放,延长 交 的延长线于点 .请直接写出线段 、 、 之间的数量关系: .28. 如图, 中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒( )
(1)、将 和 按图①方式摆放,使 经过点 ,延长 交线段 于点 .试判断线段 、 、 之间的数量关系,并证明你的结论;(2)、将 和 按图②方式摆放,延 交线段 于点 .请直接写出 、 、 之间的数量关系 .(3)、将 和 按图③方式摆放,延长 交 的延长线于点 .请直接写出线段 、 、 之间的数量关系: .28. 如图, 中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒( ) (1)、若点P在AC上,且满足PA=PB时,求出此时t的值;(2)、若点P恰好在∠BAC的角平分线上,求t的值;(3)、当t为何值时, 为等腰三角形29. 定义:有两条边长的比值为 的直角三角形叫做“半生三角形”.如图,在 中, , 是 的中点, 是 的中点, 平行AE交 于点 .
(1)、若点P在AC上,且满足PA=PB时,求出此时t的值;(2)、若点P恰好在∠BAC的角平分线上,求t的值;(3)、当t为何值时, 为等腰三角形29. 定义:有两条边长的比值为 的直角三角形叫做“半生三角形”.如图,在 中, , 是 的中点, 是 的中点, 平行AE交 于点 . (1)、当 时, 是半生三角形吗?请判断:(填“是”或“否”)(2)、当 时,求证: 是“半生三角形”;(3)、当 是“半生三角形”,且 时,求线段 的长.30. 如图,在△ABC中,∠ACB=90°,AC=BC, E为AC边的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE, CG平分∠ACB交BD于点G,
(1)、当 时, 是半生三角形吗?请判断:(填“是”或“否”)(2)、当 时,求证: 是“半生三角形”;(3)、当 是“半生三角形”,且 时,求线段 的长.30. 如图,在△ABC中,∠ACB=90°,AC=BC, E为AC边的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE, CG平分∠ACB交BD于点G, (1)、如图1,求证:CF=BG;(2)、如图2,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,
(1)、如图1,求证:CF=BG;(2)、如图2,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;
(3)、如图3,在(2)间的条件下,当∠GAC=2∠FCH时,若S△AEG=3 ,BG=6,求AC的长.