内蒙古乌兰察布市四子王旗2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 64的立方根是( )A、4 B、±4 C、8 D、±82. 下列各数: , , ,﹣1.414, ,0.1010010001…中,无理数有( )A、1个 B、2个 C、3个 D、4个3. 如果a b , 那么下列不等式不成立的是( )A、 B、 C、 D、4. 含30°角的直角三角板与直线a,b的位置关系如图所示,已知 , .则 的度数是( )
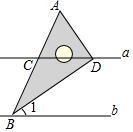 A、35° B、45° C、55° D、65°5. 下列命题中是假命题的是( )A、两点的所有连线中,线段最短 B、两条直线被第三条直线所截,同位角相等 C、等式两边加同一个数,结果仍相等 D、不等式两边加同一个数,不等号的方向不变6. 已知x轴上的点P到原点的距离为5,则点P的坐标为( )A、(5,0) B、(0,5)或(0, 5) C、(0,5) D、(5,0)或( 5,0)7. 如图,AB⊥AC,AD⊥BC,垂足为D,AB=3,AC=4,AD= ,BD= ,则点B到直线AD的距离为( )
A、35° B、45° C、55° D、65°5. 下列命题中是假命题的是( )A、两点的所有连线中,线段最短 B、两条直线被第三条直线所截,同位角相等 C、等式两边加同一个数,结果仍相等 D、不等式两边加同一个数,不等号的方向不变6. 已知x轴上的点P到原点的距离为5,则点P的坐标为( )A、(5,0) B、(0,5)或(0, 5) C、(0,5) D、(5,0)或( 5,0)7. 如图,AB⊥AC,AD⊥BC,垂足为D,AB=3,AC=4,AD= ,BD= ,则点B到直线AD的距离为( )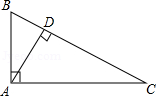 A、 B、 C、3 D、48. 如图,下列能判定AB∥EF的条件有( )
A、 B、 C、3 D、48. 如图,下列能判定AB∥EF的条件有( )①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
 A、1个 B、2个 C、3个 D、4个9. 已知方程组 的解满足x+y=2,则k的算术平方根为( )A、4 B、﹣2 C、﹣4 D、210. 为了解2018年某市参加中考的21000名学生的视力情况,从中抽查了1000名学生的视力进行统计分析,下面判断正确的是( )A、21000名学生是总体 B、上述调查是普查 C、每名学生是总体的一个个体 D、该1000名学生的视力是总体的一个样本11. 方程x+y=6的非负整数解有 ( )A、6个 B、7个 C、8个 D、无数个12. 已知点P(2a+1,1-a)在第一象限,则a的取值范围在数轴上表示正确的是( )A、
A、1个 B、2个 C、3个 D、4个9. 已知方程组 的解满足x+y=2,则k的算术平方根为( )A、4 B、﹣2 C、﹣4 D、210. 为了解2018年某市参加中考的21000名学生的视力情况,从中抽查了1000名学生的视力进行统计分析,下面判断正确的是( )A、21000名学生是总体 B、上述调查是普查 C、每名学生是总体的一个个体 D、该1000名学生的视力是总体的一个样本11. 方程x+y=6的非负整数解有 ( )A、6个 B、7个 C、8个 D、无数个12. 已知点P(2a+1,1-a)在第一象限,则a的取值范围在数轴上表示正确的是( )A、 B、
B、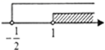 C、
C、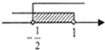 D、
D、
二、填空题
-
13. 如图,取两根木条 ,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线模型.如果∠1=15°,则∠2=15°,理由是 .
 14. 在直角坐标系中,点P(-2,3)向右平移3个单位长度后的坐标为 .15. 若 ,且n是正整数,则n= .16. 如图,直线a、b与直线c相交,且a b,∠α=105°,则∠β= .
14. 在直角坐标系中,点P(-2,3)向右平移3个单位长度后的坐标为 .15. 若 ,且n是正整数,则n= .16. 如图,直线a、b与直线c相交,且a b,∠α=105°,则∠β= .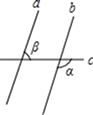 17. 若点M(a-2,a+3)在y轴上,则点N(a+2,a-3)在第象限.18. 定义运算“@”的运算法则为:x@y= ,则2@6 = .19. 已知不等式组 的解集是2<x<3,则关于x的方程ax+b=0的解为
17. 若点M(a-2,a+3)在y轴上,则点N(a+2,a-3)在第象限.18. 定义运算“@”的运算法则为:x@y= ,则2@6 = .19. 已知不等式组 的解集是2<x<3,则关于x的方程ax+b=0的解为
20. 如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别落在D′,C′的位置上,ED′与BC交于G点,若∠EFG=56°,则∠AEG=.
三、解答题
-
21. 计算:( )2+ -22. 解方程组:23. 解不等式组 并写出它的所有整数解.24. 如图,在平面直角坐标系 中, 三个顶点的坐标分别 , , 若把 向上平移 个单位长度,再向左平移 个单位长度得到 ,点 的对应点分别为 .
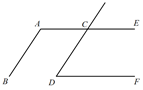
 (1)、在图中面出平移后的 ,并写出点 的坐标;(2)、求 的面积.25. 已知:如图,AB CD , 直线AE交CD于点C , ∠BAC+∠CDF=180°.
(1)、在图中面出平移后的 ,并写出点 的坐标;(2)、求 的面积.25. 已知:如图,AB CD , 直线AE交CD于点C , ∠BAC+∠CDF=180°.求证:AE DF .
 26. 某校为了了解八年级学生对S(科学)、T(技术)、E(工程)、A(艺术)、M(数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:
26. 某校为了了解八年级学生对S(科学)、T(技术)、E(工程)、A(艺术)、M(数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题: (1)、这次抽样调查共调查了多少名学生?(2)、补全条形统计图;(3)、求扇形统计图中M(数学)所对应的圆心角度数;(4)、若该校八年级学生共有400人,请根据样本数据估计该校八年级学生中对S(科学)最感兴趣的学生大约有多少人?27. 随着人们生活质量的提高,净水器已经慢慢进入了普通百姓家庭.某电器公司销售每台进价分别为2000元,1700元的A , B两种型号的净水器,下表是近两周的销售情况:
(1)、这次抽样调查共调查了多少名学生?(2)、补全条形统计图;(3)、求扇形统计图中M(数学)所对应的圆心角度数;(4)、若该校八年级学生共有400人,请根据样本数据估计该校八年级学生中对S(科学)最感兴趣的学生大约有多少人?27. 随着人们生活质量的提高,净水器已经慢慢进入了普通百姓家庭.某电器公司销售每台进价分别为2000元,1700元的A , B两种型号的净水器,下表是近两周的销售情况:销售时段
销售数量
销售收入
A型号
B型号
第一周
3台
5台
18000元
第二周
4台
10台
31000元
(1)、求A , B两种型号的净水器的销售单价;(2)、若电器公司准备用不多于54000元的金额再采购这两种型号的净水器共30台,问A型号净水器最多能采购多少台?(3)、在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.