内蒙古通辽市霍林郭勒市2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 在平面直角坐标中,点M(-2,3)在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列各式中,正确的是( )A、 B、 C、 D、3. 下列调查:(1)为了检测一批电视机的使用寿命;(2)为了调查全国平均几人拥有一部手机;(3)为了解本班学生的平均上网时间;(4)“辽宁号”航母下海前对重要零部件的检查.其中适合用抽样调查的个数有( )A、1个 B、2个 C、3个 D、4个4. 下面四个图形中,∠1与∠2是对顶角的是( )A、 B、
B、 C、
C、 D、
D、 5. 若m n , 则下列各式一定成立的是( )A、m+3 n+3 B、m﹣3 n﹣3 C、 D、﹣3m ﹣3n6. 如图,点A到线段BC的距离指的是下列哪条线段的长度( )
5. 若m n , 则下列各式一定成立的是( )A、m+3 n+3 B、m﹣3 n﹣3 C、 D、﹣3m ﹣3n6. 如图,点A到线段BC的距离指的是下列哪条线段的长度( ) A、 B、 C、 D、7. 如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是( )
A、 B、 C、 D、7. 如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是( ) A、∠1=∠2 B、∠3=∠4 C、∠2=∠4 D、∠1=∠48. 如图,一块含30°角的BC的直角顶点A在直线DE上,且BC//DE,则∠BAD等于( )
A、∠1=∠2 B、∠3=∠4 C、∠2=∠4 D、∠1=∠48. 如图,一块含30°角的BC的直角顶点A在直线DE上,且BC//DE,则∠BAD等于( ) A、30° B、45° C、60° D、90°9. 如图:
A、30° B、45° C、60° D、90°9. 如图: ,那么 的结果是( ) A、-2b B、2b C、―2a D、2a10. 如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2 , 再向正东方向走6m到达点A3 , 再向正南方向走8m到达点A4 , 再向正西方向走10m到达点A5 , 按如此规律走下去,当机器人走到点A9时,点A9在第( )象限
,那么 的结果是( ) A、-2b B、2b C、―2a D、2a10. 如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2 , 再向正东方向走6m到达点A3 , 再向正南方向走8m到达点A4 , 再向正西方向走10m到达点A5 , 按如此规律走下去,当机器人走到点A9时,点A9在第( )象限 A、一 B、二 C、三 D、四
A、一 B、二 C、三 D、四二、填空题
-
11. 某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折出售,但要保证利润率等于5%,则该商品应该打折.12. 如图,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为.
 13. 在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于x轴对称,则a+b的值为 .14. 不等式2x﹣6<0的正整数解是 .15. 若点N(x , y)在第二象限,且到x轴距离为2,到y轴距离为3,则点N的坐标是 .16. 某班有30名同学去看演出,购买甲、乙两种票共用去690元,其中甲种票每张25元,乙种票每张20元,设购买了甲种票x张,乙种票y张,由此可列出方程组 .17. 如图,把长方形ABCD沿EF对折,若∠1=500 , 则∠AEF的度数等于.
13. 在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于x轴对称,则a+b的值为 .14. 不等式2x﹣6<0的正整数解是 .15. 若点N(x , y)在第二象限,且到x轴距离为2,到y轴距离为3,则点N的坐标是 .16. 某班有30名同学去看演出,购买甲、乙两种票共用去690元,其中甲种票每张25元,乙种票每张20元,设购买了甲种票x张,乙种票y张,由此可列出方程组 .17. 如图,把长方形ABCD沿EF对折,若∠1=500 , 则∠AEF的度数等于.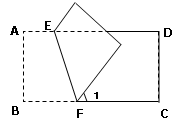 18. 已知 、 满足方程组 ,则 的值为 .
18. 已知 、 满足方程组 ,则 的值为 .三、解答题
-
19. 计算:20. 解下列方程组: .21. 解不等式组 ,并在数轴上表示解集.22. 完成以下推理过程:
如图,已知 , ,求证: .

证明: (已知)
()
()
又 (已知)
(等量代换)
()
)
23. 《教育导报》记者就四川省农村中小学教师阅读状况进行了一次问卷调查,并根据调查结果绘制了教师每年阅读书籍数量的统计图(不完整).设x表示阅读书籍的数量(x为正整数,单位:本).其中A:1⩽x⩽3; B:4⩽x⩽6; C:7⩽x⩽9;D:x⩾10.请你根据两幅图提供的信息解答下列问题: (1)、本次共调查了多少名教师?(2)、补全条形统计图;(3)、计算扇形统计图中扇形D的圆心角的度数.24. 如图,先将△ABC向上平移2个单位再向左平移5个单位得到△A1B1C1
(1)、本次共调查了多少名教师?(2)、补全条形统计图;(3)、计算扇形统计图中扇形D的圆心角的度数.24. 如图,先将△ABC向上平移2个单位再向左平移5个单位得到△A1B1C1 (1)、画出△A1B1C1 , 并写出点A1、B1、C1的坐标.(2)、求△A1B1C1的面积.25. 甲乙二人相距18千米,二人同时出发相向而行,1小时相遇;同时出发同向而行,甲3小时可以追上乙.求二人的平均速度各是多少?26. 在平面直角坐标系中,已知点 .(1)、若点M在x轴上,求m的值;(2)、若点M在第二象限内,求m的取值范围;(3)、若点M在第一、三象限的角平分线上,求m的值.27. 某小区准备新建 60 个停车位,以解决小区停车难的问题。已知新建 个地上停车位和 个地下停车位共需 1.7 万元:新建 4 个地上停车位和 2 个地下停车位共需 1.4 万元。(1)、该小区新建 1 个地上停车位和 1个地下停车位各需多少万元?(2)、若该小区新建车位的投资金额超过14 万元而不超过 15万元,问共有几种建造方案?(3)、对(2)中的几种建造方案中,哪种方案的投资最少?并求出最少投资金额.
(1)、画出△A1B1C1 , 并写出点A1、B1、C1的坐标.(2)、求△A1B1C1的面积.25. 甲乙二人相距18千米,二人同时出发相向而行,1小时相遇;同时出发同向而行,甲3小时可以追上乙.求二人的平均速度各是多少?26. 在平面直角坐标系中,已知点 .(1)、若点M在x轴上,求m的值;(2)、若点M在第二象限内,求m的取值范围;(3)、若点M在第一、三象限的角平分线上,求m的值.27. 某小区准备新建 60 个停车位,以解决小区停车难的问题。已知新建 个地上停车位和 个地下停车位共需 1.7 万元:新建 4 个地上停车位和 2 个地下停车位共需 1.4 万元。(1)、该小区新建 1 个地上停车位和 1个地下停车位各需多少万元?(2)、若该小区新建车位的投资金额超过14 万元而不超过 15万元,问共有几种建造方案?(3)、对(2)中的几种建造方案中,哪种方案的投资最少?并求出最少投资金额.