内蒙古包头市固阳县2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 9的算术平方根是( )A、±3 B、3 C、-3 D、62. 不等式组 的解集在数轴上表示为( )A、
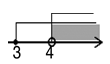 B、
B、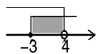 C、
C、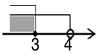 D、
D、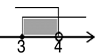 3. 下列调查活动中适合用全面调查的是( )A、“奔跑吧,兄弟”节目的收视率 B、调查乘坐飞机的旅客是否带了违禁物品 C、某种品牌节能灯的使用寿命 D、了解河北省中学生课外阅读的情况4. 下列各组数是二元一次方程组 的解的是( )A、 B、 C、 D、5. 已知a>b , 则下列不等式一定成立的是( )A、-a<-b B、a-1<b-1 C、a+2<b+2 D、2a<2b6. 如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=80°,则∠4等于( )
3. 下列调查活动中适合用全面调查的是( )A、“奔跑吧,兄弟”节目的收视率 B、调查乘坐飞机的旅客是否带了违禁物品 C、某种品牌节能灯的使用寿命 D、了解河北省中学生课外阅读的情况4. 下列各组数是二元一次方程组 的解的是( )A、 B、 C、 D、5. 已知a>b , 则下列不等式一定成立的是( )A、-a<-b B、a-1<b-1 C、a+2<b+2 D、2a<2b6. 如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=80°,则∠4等于( )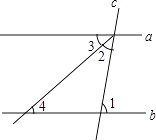 A、20° B、40° C、60° D、80°7. 在平面直角坐标系中,将点A(m-1,n+2)先向右平移3个单位,再向上平移2个单位,得到点A′.若点A′位于第二象限,则m、n的取值范围分别是( )A、m<0,n>0 B、m<0,n<-2 C、m<-2,n>-4 D、m<1,n>-28. 从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走 ,平路每小时走 .下坡每小时走 ,那么从甲地到乙地需 ,从乙地到甲地需 .设从甲地到乙地的上坡路程长 ,平路路程长为 ,依题意列方程组正确的是( )A、 B、 C、 D、9. 一宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团15人准备同时租用这三种客房共5间,如果每个房间都住满,租房方案有( )A、4种 B、3种 C、2种 D、1种10. 对于有理数a、b , 定义min{a , b}的含义为:当a<b时,min{a , b}=a , 例如:min{1,-2}=-2.已知min{ ,a}=a , min{ ,b}= ,且a和b为两个连续正整数,则a-b的立方根为( )A、-1 B、1 C、-2 D、2
A、20° B、40° C、60° D、80°7. 在平面直角坐标系中,将点A(m-1,n+2)先向右平移3个单位,再向上平移2个单位,得到点A′.若点A′位于第二象限,则m、n的取值范围分别是( )A、m<0,n>0 B、m<0,n<-2 C、m<-2,n>-4 D、m<1,n>-28. 从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走 ,平路每小时走 .下坡每小时走 ,那么从甲地到乙地需 ,从乙地到甲地需 .设从甲地到乙地的上坡路程长 ,平路路程长为 ,依题意列方程组正确的是( )A、 B、 C、 D、9. 一宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团15人准备同时租用这三种客房共5间,如果每个房间都住满,租房方案有( )A、4种 B、3种 C、2种 D、1种10. 对于有理数a、b , 定义min{a , b}的含义为:当a<b时,min{a , b}=a , 例如:min{1,-2}=-2.已知min{ ,a}=a , min{ ,b}= ,且a和b为两个连续正整数,则a-b的立方根为( )A、-1 B、1 C、-2 D、2二、填空题
-
11. 的绝对值是 .12. 若点M(a-3,a+4)在y轴上,则a=.13. 已知x和y满足方程组 ,则x-y的值为。14. 如图,不添加辅助线,请写出一个能判定 ∥ 的条件.
 15. 若关于 的不等式组 只有4个正整数解,则 的取值范围为.16. 在长为 、宽为 的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则每个小长方形花圃的面积是 .
15. 若关于 的不等式组 只有4个正整数解,则 的取值范围为.16. 在长为 、宽为 的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则每个小长方形花圃的面积是 . 17. 观察下列等式:
17. 观察下列等式:① 32 - 12 = 2 × 4
② 52 - 32 = 2 × 8
③ 72 - 52 = 2 × 12
......
那么第n(n为正整数)个等式为
三、解答题
-
18. 解方程组:(1)、(2)、19. 解不等式(组),并在数轴上表示解集:(1)、(2)、20. 七年级数学研究学习小组在某十字路口随机调查部分市民对“社会主义核心价值观”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:


 (1)、本次调查的总人数为人,在扇形统计图中“C”所在扇形的圆心角的度数为;(2)、补全频数分布图;(3)、若在这一周里,该路口共有20000人通过,请估计得分超过80的大约有多少人?21. 如图,已知∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上.
(1)、本次调查的总人数为人,在扇形统计图中“C”所在扇形的圆心角的度数为;(2)、补全频数分布图;(3)、若在这一周里,该路口共有20000人通过,请估计得分超过80的大约有多少人?21. 如图,已知∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上. (1)、求证:CD∥AB;(2)、若∠A=∠ACB+30°,求∠D的度数.22. 某小区准备新建50个停车位,以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.5万元;新建3个地上停车位和2个地下停车位共需1.1万元.(1)、该小区新建1个地上停车位和1个地下停车位各需多少万元?(2)、若该小区预计投资金额超过10万元,且地上的停车位要求不少于30个,问共有几种建造方案?(3)、对(2)中的几种建造方案中,哪一个方案的投资最少?并求出最少投资金额.23. 已知:点E、点G分别在直线AB、直线CD上,点F在两直线外,连接EF、FG.(1)、如图1,AB∥CD,求证:∠AEF+∠FGC=∠EFG;
(1)、求证:CD∥AB;(2)、若∠A=∠ACB+30°,求∠D的度数.22. 某小区准备新建50个停车位,以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.5万元;新建3个地上停车位和2个地下停车位共需1.1万元.(1)、该小区新建1个地上停车位和1个地下停车位各需多少万元?(2)、若该小区预计投资金额超过10万元,且地上的停车位要求不少于30个,问共有几种建造方案?(3)、对(2)中的几种建造方案中,哪一个方案的投资最少?并求出最少投资金额.23. 已知:点E、点G分别在直线AB、直线CD上,点F在两直线外,连接EF、FG.(1)、如图1,AB∥CD,求证:∠AEF+∠FGC=∠EFG; (2)、若直线AB与直线CD不平行,连接EG,且EG同时平分∠BEF和∠FGD 如图2,请探索∠AEF、∠FGC、∠EFG之间的数量关系?并说明理由.
(2)、若直线AB与直线CD不平行,连接EG,且EG同时平分∠BEF和∠FGD 如图2,请探索∠AEF、∠FGC、∠EFG之间的数量关系?并说明理由.