辽宁省锦州市凌海市2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算结果正确的是（）

A、3x+2x＝5x² B、（﹣a³b）²＝a⁶b² C、﹣m²•m⁴＝m⁶ D、（a³）³＝a⁶

查看试题解析
2. 下面每组数分别是三根小木棒的长度，用它们不能摆成一个三角形的是（　　）

A、5cm ， 10cm ， 5cm B、7cm ， 8cm ， 9cm C、3cm ， 4cm ， 5cm D、6cm ， 20cm ， 20cm

查看试题解析
3. 在下列交通标志图案中，具有轴对称性质的图案是（）

A、 B、 C、 D、

查看试题解析
4. 在七年（1）与七年（2）班举行拔河比赛前，根据双方的实力，环环预测：“七年（1）获胜的机会是80%”，那么下面四个说法正确的是（）

A、七年（2）班肯定会输掉这场比赛 B、七年（1）班肯定会赢得这场比赛 C、若比赛10次，则七年（1）班会赢得8次 D、七年（2）班也有可能会赢得这场比赛

查看试题解析
5. 如图，下面图象（折线OEFPMN）描述了某汽车在行驶过程中速度与时间之间的关系，下列说法中错误的是（）

A、第3分钟时汽车的速度是40千米/小时 B、第12分钟时汽车的速度是0千米/小时 C、从第3分钟后到第6分钟，汽车停止不动 D、从第9分钟到第12分钟，汽车速度从60千米/小时减少到0千米/小时

查看试题解析
6. 将一直角三角板与两边平行的纸条如图放置．已知∠1=30°，则∠2的度数为（）

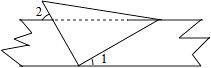A、30° B、45° C、50° D、60°

查看试题解析
7. 在正方形网格中，∠AOB的位置如图所示，则点P、Q、M、N中在∠AOB的平分线上是（）

A、P点 B、Q点 C、M点 D、N点

查看试题解析
8. 如图，为了测量B点到河对面的目标A之间的距离，在B点同侧选择了一点C，测得∠ABC＝75°，∠ACB＝35°，然后在M处立了标杆，使∠CBM＝75°，∠MCB＝35°，得到 $△$ MBC≌ $△$ ABC，所以测得MB的长就是A，B两点间的距离，这里判定 $△$ MBC≌ $△$ ABC的理由是（）

A、SAS B、AAA C、SSS D、ASA

查看试题解析

二、填空题

9. 世界上最小的开花结果植物是澳大利亚的出水浮萍，其果实质量只有 0. 00 000 0076 克，用科学记数法表示是克.

查看试题解析
10. 如图，直线AB，CD，EF相交于点O，AB⊥CD，OG平分∠AOE，∠FOD＝30°，则∠BOE＝度，∠AOG＝度．

查看试题解析
11. 若4^x=2，4^y=3，则4^x+y=。

查看试题解析
12. 在一定条件下，若物体运动的路程S（米）与时间t（秒）的关系式为S＝3t²+2t+1，则当t＝3时，该物体所经过的路程为．

查看试题解析
13. 如图，点E在AD的延长线上，下列四个条件：①∠3=∠4；②∠1=∠2；③∠A=∠5；④∠C+∠ABC=180°.能判定AB∥CD的条件是（填序号）

查看试题解析
14. 小明将飞镖随意投中如图所示的正方体木框中，那么投中阴影部分的概率为．

查看试题解析
15. 如图 $△$ ABC中，AD是BC上的中线，CE是 $△$ ACD中AD边上的中线，若 $△$ ABC的面积是24，则 $△$ ACD的面积是， $△$ ACE的面积是．

查看试题解析
16. 某电影院地面的一部分为扇形，观众席的座位数按下列方式设置：

排数（x）

1

2

3

4

……

座位数（y）

40

43

46

49

……

若排数x是自变量，y是因变量，则y与x之间的函数关系式为．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(\frac{2}{3})}^{- 2} \cdot {(- 4)}^{2} - {(30 - 4.5)}^{0}$ ；

(2)、 $x y \cdot {(2 x y^{2})}^{3} \div (\frac{1}{2} x^{2} y)$ ．

查看试题解析
18. 先化简，再求值：（x+4）²﹣（x﹣4）² ，其中 $x = \frac{1}{8}$ ．

查看试题解析
19. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ．请用尺规作图法在 $A C$ 上找一点D，使得点D到 $A B$ 的距离等于 $D C$ ．（保留作图痕迹，不写作法）

查看试题解析
20. 某人制成了一个如图所示的游戏转盘，转盘被分成8个相同的扇形，取名为“开心转转转”．游戏规定：参与者自由转动转盘，转盘停止后，若指针指向字母“A”，则参与者交费2元；若指针指向字母“B”，则参与者获奖3元，若指针指向字母“C”，则参与者获奖1元．那么任意转动转盘一次，转盘停止后，参与者交费2元、参与者获奖3元、参与者获奖1元的概率各为多少？

查看试题解析
21. 如图，B是AC中点，∠F=∠E，∠1=∠2．证明：AE=CF．

查看试题解析
22. 如图，点P是∠AOB外的一点，点Q与P关于OA对称，点R与P关于OB对称，直线QR分别交OA、OB于点M、N，若PM＝PN＝4，MN＝5．

(1)、求线段QM、QN的长；

(2)、求线段QR的长．

查看试题解析
23. 甲、乙两人沿相同的路线骑行由A地到B地，骑行过程中路程与时间关系的图象如图所示．根据图象解答下列问题：

(1)、甲、乙两人谁先到达终点？先到多长时间？

(2)、分别求出甲、乙两人的行驶速度；

(3)、在什么时间段内，两人均行驶在途中？（不包括起点和终点）

(4)、当甲、乙两人途中相遇时，直接写出相遇地与A地的距离．

查看试题解析
24. 在 $△$ ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．

(1)、如图1所示位置时判断 $△$ ADC与 $△$ CEB是否全等，并说明理由；

(2)、如图2所示位置时判断 $△$ ADC与 $△$ CEB是否全等，并说明理由．

查看试题解析

排数（x）	1	2	3	4	……
座位数（y）	40	43	46	49	……