辽宁省大连市庄河市2019-2020学年七年级下学期数学期末试卷
试卷更新日期：2021-04-28 类型：期末考试
一、单选题
-
1. 9的平方根是（ ）．A、3 B、±3 C、 D、±812. 如图，直线a ， b相交于点O ， 若∠1＝40°，则∠2＝（ ）
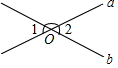A、40° B、50° C、60° D、140°3. 下列调查中，适宜采用全面调查（普查）方式的是（ ）A、调查市场上老酸奶的质量情况 B、调查某品牌圆珠笔芯的使用寿命 C、调查乘坐飞机的旅客是否携带了危禁物品 D、调查我市市民对新冠病毒的知晓率4. 下列各点，在第二象限的是（ ）A、（﹣2，﹣1） B、（﹣2，1） C、（2，﹣1） D、（2，1）5. 如图，直线a，b被直线c所截，下列条件不能判定直线a与b平行的是（ ）
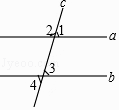A、∠1=∠3 B、∠2+∠4=180° C、∠1=∠4 D、∠3=∠46. 已知a＜b，下列结论正确的是（ ）A、a+m＞b+m B、a-m＞b-m C、-2a＞-2b D、7. 如图，直线AB和CD交于点O，OA平分∠EOC，若∠EOC＝70°，则∠BOD的度数为（ ）
A、70° B、35° C、30° D、110°8. 已知 ,则a+b等于（ ）A、2 B、 C、3 D、19. 一个正方形的面积是12，估计它的边长大小在（ ）
A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间10. 如图，∠BCD＝70°，AB∥DE ， 则∠α与∠β满足（ ）
A、∠α+∠β＝110° B、∠α+∠β＝70° C、∠β﹣∠α＝70° D、∠α+∠β＝90°二、填空题
-
11. 计算： = ．12. 不等式﹣x+2≤0的解集是 ．13. 某校学生来自A、B、C三个地区，其人数比是2：5：3，如图，扇形图表示上述分布情况，代表C地区扇形圆心角是 ．
14. 如图，AB∥CD，BC平分∠ABD，且∠C＝40°，则∠D的度数是 ．
15. 在平面直角坐标系xOy中，点A ， B的坐标分别为（﹣4，3），（﹣1，3），将线段AB沿x轴正方向平移m个单位，若线段AB与y轴有交点，则m的取值范围为是 ．三、解答题
-
16.
如图所示，在象棋盘上建立平面直角坐标系，使使“马”位于点（2，2），“炮”位于点（﹣1，2），写出“兵”所在位置的坐标．
17. 计算：18. 解不等式组： ，并把它的解集在下面数轴上表示出来．
19. 如图所示，直线a、b被c、d所截，且a⊥c，b⊥c，∠1=70°，求∠3的度数．
20. 七年一班学习小组的同学为了解2020年某小区家庭月平均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理．用水量分组
频数
百分比
0＜x≤5
6
12%
5＜x≤10
m
24%
10＜x≤15
16
32%
15＜x≤20
10
20%
20＜x≤25
4
n
25＜x≤30
2
4%
请解答以下问题：
(1)、填空：m＝ ， n＝；(2)、把频数分布直方图补充完整；(3)、若该小区有1000户家庭，根据调查数据估计，该小区月平均用水量超过20t的家庭的户数．21. 3辆小卡车和5辆大卡车一次可运货物31吨，4辆小卡车和3辆大卡车一次可运货物23吨，则小卡车和大卡车每辆每次可以各运货物多少吨？22. 如图，在平面直角坐标系中，已知点A(－3，3)，B(－5，1)，C(－2，0)，P(a，b)是△ABC的边AC上任意一点，△ABC经过平移后得到△A1B1C1 ， 点P的对应点为P1(a＋6，b－2)．
(1)、直接写出点C1的坐标；(2)、在图中画出△A1B1C1；(3)、求△AOA1的面积．23. 如图，点E在BC上，∠A＝∠D ， ∠ACB与∠BED互补．求证：AB∥CD ．
24. 去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．(1)、求饮用水和蔬菜各有多少件？(2)、现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；(3)、在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？25. 如图，正方形OABC边长为20，点D的坐标为( ，0)，且 以OD、DE为邻边作长方形ODEF.
(1)、请直接写出以下点的坐标：E ， F(用含 的式子表示)；(2)、设长方形ODEF与正方形OABC重叠部分面积为S，求S(用含 的式子表示)；(3)、S的值能否等于300，若能请求出此时 的值；若不能，请说明理由。