江西省宜春市高安市2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运动属于平移的是（）

A、荡秋千 B、地球绕着太阳转 C、风筝在空中随风飘动 D、急刹车时，汽车在地面上的滑动

查看试题解析
2. $\sqrt{64}$ 的立方根是（　　）

A、±2 B、±4 C、4 D、2

查看试题解析
3. 如果 $a > b$ ，那么下列结论一定正确的是（）

A、 $a^{2} > b^{2}$ B、 $3 - a > 3 - b$ C、 $a c^{2} > b c^{2}$ D、 $- \frac{a}{3} < - \frac{b}{3}$

查看试题解析
4. 如图，现给出下列条件：① $∠ 1 = ∠ B$ ，② $∠ 2 = ∠ 5$ ，③ $∠ 3 = ∠ 4$ ，④ $∠ B C D + ∠ D = 180^{°}$ ．⑤ $∠ B + ∠ B C D = 180^{°}$ ，其中能够得到 $A B / / C D$ 的条件有（）

A、①②④ B、①③⑤ C、①②⑤ D、①②④⑤

查看试题解析
5. 若关于x的一元一次不等式组 ${\begin{array}{l} 3 - 2 x > 1 \\ x - a > 0 \end{array}$ 恰有 $3$ 个整数解，那么a的取值范围是（）

A、 $- 2 < a < 1$ B、 $- 3 < a \leq - 2$ C、 $- 3 \leq a < - 2$ D、 $- 3 < a < - 2$

查看试题解析
6. 某地区经过两年的产业扶贫后，经济总收入增加了一倍．为更好地了解该地区的经济收入变化情况，统计了产业扶贫前后的经济收入相关数据，得到下列统计图：下面结论错误的是（）

A、经过产业扶贫后．养殖收入增加了一倍 B、经过产业扶贫后，种植收入减少了 C、经过产业共贫后，养殖收入与第二产业收入的总和超过了经济收入的一半 D、经过产业扶贫后．其他收入增加了一倍以上

查看试题解析

二、填空题

7. 将方程2x﹣3y＝5变形为用x的代数式表示y的形式是．

查看试题解析
8. 若点 $(1 - 2 m ， m - 4)$ 在第二象限内，则m的取值范围是

查看试题解析
9. 如图，折叠宽度相等的长方形纸条，若∠1=62°，则∠2=度

查看试题解析
10. 已知 $a 、 b$ 为两个连续的整数，且 $a < \sqrt{11} < b$ ，则 $a + b$ = .

查看试题解析
11. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托.折回索子却量竿，却比竿子短一托.”其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺.设绳索长x尺，竿长y尺，则正确的方程组是

查看试题解析
12. 平行四边形的三个顶点坐标 $A (0 ， 0) 、 B (4 ， 0) 、 C (2 ， 4)$ ，则第四个顶点D的坐标是

查看试题解析

三、解答题

13.

(1)、解方程 ${\begin{array}{l} 3 x - y = 7 \\ x + 3 y = - 1 \end{array}$

(2)、如图所示，直线 $a ， b$ 被 $c ， d$ 所截，且 $c ⊥ a ， c ⊥ b ， ∠ 1 = 70^{°}$ ，求 $∠ 3$ 的大小．

查看试题解析
14. 解不等式组： ${\begin{array}{l} \frac{x - 3}{2} + 3 \geq x + 1 \\ 1 - 3 (x - 1) < 8 - x \end{array}$ 并在数轴上把解集表示出来．

查看试题解析
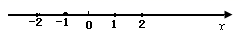15. 如图所示，某住宅小区内有一块长的长 $32 m$ ，宽 $20 m$ 方形形，想在长方形地块内修筑同样宽的两条“之”字路，余下的部分做绿化，道路的宽为 $2$ 米，求绿化的面积．

查看试题解析
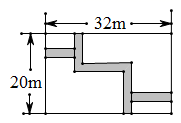16. 图中标明了李明同学家附近的一些地方，已知李明同学家位于（-2，-1）．

(1)、建立平面直角坐标系，写出学校，邮局的坐标；

(2)、某星期日早晨，李明同学从家里出发，沿着（-1，-2）、（1，-2）、（2，-1）、（1，-1）、（1，3）、（-1，0）、（0，-1）的路线转了一下，写出他路上经过的地方；

(3)、连接他在（2）中经过的地点，你能得到什么图形？

查看试题解析
17. 如图是一个安全用电标记图案．可以抽象为图（2）的几何图形．其中 $A B / / D C ， B E / / F C$ ．点 $E ， F$ 在 $A D$ 上．若 $∠ A = 15^{°} ， ∠ B = 60^{°}$ ，求 $∠ A F C$ 的度数．

查看试题解析
18. 已知方程组的 ${\begin{array}{l} 2 x - y = 4 a \\ x - 2 y = 2 a + 3 \end{array}$ 的解满足 $x > y .$ 求a的取值范围．

查看试题解析

19. 为了解江西某县城区学生在中考体育测试各项目的报考与成绩情况，调研组随机抽取了城区一所初中（城区各初中的人数和体育素养相当），对该所初中的上届

1400

名毕业生中考体育的相关情况进行了调查．中考体育测试项目有①必考项目：男生

1000 m

（记为C）、女生

800 m

（记为

C'

）；男生

1

分钟跳绳（记为D）、女生

1

分钟跳绳（记为

D'

）．②选考项目（二选一）：男生立定跳远（记为E），女生立定跳远（记为

E'

）；男生引体向上（记为F），女生仰卧起坐（记为

F'

），根据调查结果绘制了如下统计图表．

得分频数分布表

得分x/分	频数
得分x/分	男生	女生
$51 < x \leq 55$	500
$47 < x \leq 51$		160
$43 < x \leq 47$	100	100
$39 < x \leq 43$	0	40

请根据图中信息解答下列问题：

(1)、设该校男生有x人，女生有y人，在这项调查中，该校女生“仰卧起坐”人数是男生“引体向上”人数的

21

倍，求

x ， y

的值．

(2)、并请完成得分频数分布表．

(3)、该县城区初中上届参加中考体育测试的共有4000人，如果把47分以上（不含47分）的体育成绩定为合格，估计合格率是百分之几?据此可估计其中有多少学生体育成绩合格?（精确到个位）

查看试题解析

20. 小明同学在做作业时，遇到这样一道几何题：
已知：如图1，l₁∥l₂∥l₃ ，点A、M、B分别在直线l₁ ， l₂ ， l₃上，MC平分∠AMB，∠1=28°，∠2=70°．求：∠CMD的度数．

小明想了许久没有思路，就去请教好朋友小坚，小坚给了他如图2所示的提示：

请问小坚的提示中①是∠ ， ④是∠ ．

理由②是：；

理由③是：；

∠CMD的度数是°．

查看试题解析
21. 如图所示的直角坐标系中， $Δ A B C$ 的顶点坐标分别是 $A (1 ， 0) B (- 2 ， 3) ， C (- 3 ， 0) .$

⑴在平面直角坐标系中画出 $Δ A B C$ ，并求 $Δ A B C$ 的面积：

⑵如果将 $Δ A B C$ 向右平移 $3$ 个单位长度，再向下平移 $2$ 个单位长度，得到 $Δ A_{1} B_{1} C_{1}$ ．画出 $Δ A_{1} B_{1} C_{1}$ ，并试求出 $A_{1} ， B_{1} ， C_{1}$ 的坐标．

⑶若点 $A ， C$ 的位置不变，当点P在什么位置时，使 $S_{Δ A C P} = S_{Δ A B C}$

⑷若点 $B 、 C$ 的位置不变，当点Q在x轴上什么位置时，使 $S_{Δ A B C} = 2 S_{Δ Q B C} .$

查看试题解析
22. 对非负实数x“四舍五入”到个位的值记为[x]．即当n为非负整数时，若 $n - \frac{1}{2} \leq x < n + \frac{1}{2}$ ，则[x]=n．如： [3.4]=3， [3.5]=4．根据以上材料，解决下列问题：

(1)、填空：①若[x]=3，则x应满足的条件：；②若[3x+1]=3，则x应满足的条件：；

(2)、求满足[x]= $\frac{5}{3}$ x-1的所有非负实数x的值(要求书写解答过程)．

查看试题解析
23. 直线EF、GH之间有一个直角三角形ABC，其中∠BAC = 90°，∠ABC = ．

(1)、如图1，点A在直线EF上，B、C在直线GH上，若∠ =60°，∠FAC =30°．求证：EF∥GH；

(2)、将三角形ABC如图2放置，直线EF∥GH，点C 、B分别在直线EF、GH上，且BC平分∠ABH，直线CD平分∠FCA交直线GH于D．在取不同数值时，∠BCD的大小是否发生变化？若不变求其值，若变化指出其变化范围．

查看试题解析