江西省宜春市2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $A (3, - 5)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列调查活动中，适合全面调查的是（）

A、对某班同学“防疫知识”掌握度的调查 B、对某品牌口罩合格率的调查 C、对“十三届全国人大一次会议开幕式”在线收视率的调查 D、对秀江水质情况的调查

查看试题解析
3. 下列实数中： $\sqrt{9}$ 、 $\sqrt{7}$ 、2.15、 $\frac{11}{7}$ 、 $π$ 、0.3030030003…（往后每两个3之间依次多一个0），无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 将一直角三角板与等宽的纸条如图放置，顶点C在纸条边FG上，且DE//FG，当 $∠ 1 = 32 °$ 时，∠2的度数是（）

A、48° B、32° C、58° D、64°

查看试题解析
5. 若关于 $x$ 的不等式 ${\begin{matrix} x > a - 1 \\ 3 x \leq 2 (x + 2) \end{matrix}$ 仅有四个整数解，则a的取值范围是（）

A、 $1 \leq a \leq 2$ B、 $1 \leq a < 2$ C、 $1 < a < 2$ D、 $a < 2$

查看试题解析
6. 如图，动点P在平面直角坐标系中，沿曲线的方向从左往右运动，第1秒从原点运动到点（1，1），第2秒运动到点（2，0），第3秒运动到点（3，-1），第4秒运动到点（4，0）……按这样的规律，第2020秒运动到点（）

A、（2020，1） B、（2020，－1） C、（2020，0） D、（2019，0）

查看试题解析

二、填空题

7. 9的算术平方根是．

查看试题解析
8. 若 $\sqrt{3 x - 6} + | y - 2 x + 1 | = 0$ ，则x+y= ．

查看试题解析
9. 《九章算术》中记载：“今有甲乙二人持钱不知其数，甲得乙半而钱五十，乙得甲太半而钱亦五十，问甲、乙持钱各几何？”译文：“假设有甲乙二人，不知其钱包里有多少钱，若乙把自己一半的钱给甲，则甲的钱数为50；而甲把自己 $\frac{2}{3}$ 的钱给乙，则乙的钱数也能为50．问甲、乙各有多少钱？”设甲持钱数为x，乙持钱数为y，可列方程组为．

查看试题解析
10. 如图，直线EF、CD相交于点O，OA⊥OB，OC平分∠AOF，若∠AOE=40°，则∠BOD= ．

查看试题解析
11. 关于x、y的二元一次方程组 ${\begin{matrix} 3 x + y = 3 m + 1 \\ x + 2 y = 3 \end{matrix}$ 的解满足不等式 $2 x - y < 1$ ，则m的取值范围是．

查看试题解析
12. 如图， $∠ A O C = ∠ B O D = 90 °$ ， $∠ A O B = 70 °$ ，在∠AOB内画一条射线OP得到的图中有m对互余的角，其中 $∠ A O P = x °$ ，且满足 $0 < x < 50$ ，则 $m =$ ．

查看试题解析

三、解答题

13.

(1)、计算： $| 1 - \sqrt{3} | - \sqrt{{(- 2)}^{2}} \times \frac{1}{2} + \sqrt[3]{8}$ ；

(2)、解方程组： ${\begin{array}{l} 2 x + 3 y = 7 \\ x - y = 1 \end{array}$ ．

查看试题解析
14. 解不等式组： ${\begin{array}{l} x - 2 (x - 1) < 3 \\ 5 x - 4 < 3 x + 2 \end{array}$ ，并将解集在数轴上表示出来．

查看试题解析
15.

(1)、解不等式 $\frac{3 x + 1}{2} - \frac{4 x}{3} > 1$ ；

(2)、若（1）中的不等式的最小整数解是方程 $3 x + a x = 5$ 的解，求a的值．

查看试题解析
16. 如图，在平面直角坐标系中，点A、B、C的坐标分别为 $A (2 ， - 1)$ ， $B (4 ， 3)$ ， $C (1 ， 2)$ ．将 $Δ A B C$ 先向左平移4个单位，再向下平移2个单位得到 $Δ A_{1} B_{1} C_{1}$ ．

(1)、请在图中画出 $Δ A_{1} B_{1} C_{1}$ ；

(2)、写出平移后的 $Δ A_{1} B_{1} C_{1}$ 三个顶点的坐标： $A_{1}$ （，） $B_{1}$ （，） $C_{1}$ （，）

(3)、求 $Δ A B C$ 的面积．

查看试题解析
17. 某校为了解疫情期间学生在家上网课的学习情况，随机抽取了该校部分学生对其学习效果进行调查，根据相关数据，绘制成以下不完整的统计图．

(1)、此次调查该校学生人数为名，学习效果“较差”的部分对应的圆心角度数为；

(2)、补全条形图；

(3)、请估计该校3000名学生疫情期间网课学习效果“一般”的学生人数．

查看试题解析
18. 如图，已知点E在直线DC上，射线EF平分∠AED，过E点作EB⊥EF，G为射线EC上一点，连结BG，且 $∠ E B G + ∠ B E G = 90 °$ ．

(1)、求证： $∠ D E F = ∠ E B G$ ；

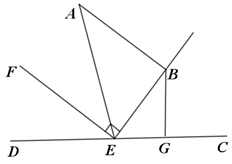(2)、若 $∠ E B G = ∠ A$ ，试判断AB与EF的位置关系，并说明理由．

查看试题解析
19. 对于两个数a、b，我们定义：① $M (a ， b)$ 表示这两个数的平均数，例如： $M (- 1 ， 3) = \frac{- 1 + 3}{2} = 1$ ；
② $\max (a ， b)$ 表示这两个数中更大的数，当 $a \geq b$ 时， $\max (a ， b) = a$ ；当 $a < b$ 时， $\max (a ， b) = b$ ：例如： $\max (- 1 ， 3) = 3$ ．根据以上材料，解决下列问题：

(1)、 $M (2020 ， 0) =$ ， $\max (2020 ， 0) =$ ；

(2)、若 $M (6 - 2 x ， 2) = \max (6 - 2 x ， 2)$ ，求x的值．

查看试题解析
20. 某小区为激励更多居民积极参与“分类适宜，垃圾逢春”活动，决定购买拖把和扫帚作为奖品，奖励给垃圾分类表现优异的居民．若购买3把拖把和2把扫帚共需80元，购买2把拖把和1把扫帚共需50元．

(1)、请问拖把和扫帚每把各多少元？

(2)、现准备购买拖把和扫帚共200把，且要求购买拖把的费用不低于购买扫帚的费用，所有购买的资金不超过2690元，问有几种购买方案，哪种方案最省钱？

查看试题解析
21. （阅读材料）：
①在 $Δ A B C$ 中，若 $∠ C = 90 °$ ，由“三角形内角和为180°”得 $∠ A + ∠ B = 180 ° - ∠ C = 180 ° - 90 ° = 90 °$ ．

②在 $Δ A B C$ 中，若 $∠ A + ∠ B = 90 °$ ，由“三角形内角和为180°”得 $∠ C = 180 ° - (∠ A + ∠ B) = 180 ° - 90 ° = 90 °$ ．

（解决问题）：

如图①，在平面直角坐标系中，点C是x轴负半轴上的一个动点．已知 $A B / / x$ 轴，交y轴于点E，连接CE，CF是∠ECO的角平分线，交AB于点F，交y轴于点D．过E点作EM平分∠CEB，交CF于点M．

(1)、试判断EM与CF的位置关系，并说明理由；

(2)、如图②，过E点作PE⊥CE，交CF于点P．求证：∠EPC=∠EDP；

(3)、在（2）的基础上，作EN平分∠AEP，交OC于点N，如图③．请问随着C点的运动，∠NEM的度数是否发生变化？若不变，求出其值：若变化，请说明理由．

查看试题解析