江西省赣州市大余县2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 下列各实数中,最小的实数是( )A、0 B、 C、-2 D、2. 下面四个图形中, 与 是邻补角的是( )A、
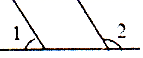 B、
B、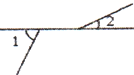 C、
C、 D、
D、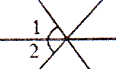 3. 下列调查中,调查方式选择正确的是( )A、为了了解一批灯泡的使用寿命,选择全面调查; B、为了了解某班同学的身高情况,选择抽样调查; C、为了了解航天飞机各个零件是否安全,选择全面调查; D、为了了解生产的一批炮弹的杀伤半径,选择全面调查.4. 如果 ,那么下列结论一定正确的是( )A、 B、 C、 D、5. 已知 ,则a-b等于( )A、4 B、5 C、6 D、76. 对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次停止,那么x的取值范围是()
3. 下列调查中,调查方式选择正确的是( )A、为了了解一批灯泡的使用寿命,选择全面调查; B、为了了解某班同学的身高情况,选择抽样调查; C、为了了解航天飞机各个零件是否安全,选择全面调查; D、为了了解生产的一批炮弹的杀伤半径,选择全面调查.4. 如果 ,那么下列结论一定正确的是( )A、 B、 C、 D、5. 已知 ,则a-b等于( )A、4 B、5 C、6 D、76. 对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次停止,那么x的取值范围是() A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
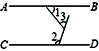
7. 已知点A在x轴上方,y轴左侧,到x轴的距离是3,到y轴的距离是4,那么点A的坐标是 .8. 已知点A(-1,b+2)在坐标轴上,则b= .9. 如图,AB∥CD,∠1=50°,∠2=110°,则∠3=度.
 10. 我国古代数学著作《九章算术》的“方程”一章里,一次方程组是由算筹布置而成的.如图①,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项,把图①所示的算筹图用我们现在所熟悉的方程组的形式表述出来,就是 .请你根据图②所示的算筹图,可列出方程组为 .
10. 我国古代数学著作《九章算术》的“方程”一章里,一次方程组是由算筹布置而成的.如图①,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项,把图①所示的算筹图用我们现在所熟悉的方程组的形式表述出来,就是 .请你根据图②所示的算筹图,可列出方程组为 . 11. 如图,三角形ABC中,∠BAC=70°, D是射线BC上一点(不与点B,C重合),DE∥AB交直线AC于E,DF∥AC交直线AB于F,则∠FDE的度数为.
11. 如图,三角形ABC中,∠BAC=70°, D是射线BC上一点(不与点B,C重合),DE∥AB交直线AC于E,DF∥AC交直线AB于F,则∠FDE的度数为.
三、解答题
-
12. 计算13. 解方程组 .14. 解不等式组 ,并把解集在数轴上表示出来.
 15. 如图:∠1=∠2=45°,∠3=100°,求∠4的度数.
15. 如图:∠1=∠2=45°,∠3=100°,求∠4的度数. 16. 如图,在数轴上,点 、 分别表示数 、 .
16. 如图,在数轴上,点 、 分别表示数 、 . (1)、求 的取值范围.(2)、数轴上表示数 的点应落在( )A、点 的左边 B、线段 上 C、点 的右边17. 如图,△ABC在直角坐标系中,
(1)、求 的取值范围.(2)、数轴上表示数 的点应落在( )A、点 的左边 B、线段 上 C、点 的右边17. 如图,△ABC在直角坐标系中, (1)、请写出△ABC各点的坐标.(2)、求出(3)、若把△ABC向上平移2个单位,再向右平移3个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.18. 章太炎先生有一句话:“夫国学者,国家所以成立之源泉也.“为了激发学生学习国学经典的热情,弘扬文明风尚,某学校以“书香飘溢校园•国学浸润心灵“为主题,开展国学经典系列比赛项目:A读经典,B写经典,C唱经典,D演经典,为了解学生对这四个项目的报名参赛情况(每名学生选报一个项目),学校随机抽取了部分学生进行“你选择参加哪一项经典比赛活动”的调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据图中的信息解答下列问题.
(1)、请写出△ABC各点的坐标.(2)、求出(3)、若把△ABC向上平移2个单位,再向右平移3个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.18. 章太炎先生有一句话:“夫国学者,国家所以成立之源泉也.“为了激发学生学习国学经典的热情,弘扬文明风尚,某学校以“书香飘溢校园•国学浸润心灵“为主题,开展国学经典系列比赛项目:A读经典,B写经典,C唱经典,D演经典,为了解学生对这四个项目的报名参赛情况(每名学生选报一个项目),学校随机抽取了部分学生进行“你选择参加哪一项经典比赛活动”的调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据图中的信息解答下列问题. (1)、填空:在条形统计图中,m= , n=;(2)、求在扇形统计图中,“C“项目所在扇形的圆心角的度数;(3)、若该学校共有学生4800名,请根据抽样调查的结果,估计学校将有多少人参加“D“项目比赛活动?19. 因“抗击疫情”需要,学校决定购买A型和B型测温枪,已知购进三把A型测温枪和两把B型测温枪共需1900元,购进两把A型测温枪和三把B型测温枪共需2100元.(1)、一把A型测温枪和一把B型测温枪的售价分别是多少元?(2)、根据学校实际情况,学校共需测温枪30把,县教科体局给学校的预算为1万元,为了不超出预算,学校最多可购进B型测温枪多少?20. 在平面直角坐标系中,A(a,0),B(b,0),C(−1,2),且| |+ =0,
(1)、填空:在条形统计图中,m= , n=;(2)、求在扇形统计图中,“C“项目所在扇形的圆心角的度数;(3)、若该学校共有学生4800名,请根据抽样调查的结果,估计学校将有多少人参加“D“项目比赛活动?19. 因“抗击疫情”需要,学校决定购买A型和B型测温枪,已知购进三把A型测温枪和两把B型测温枪共需1900元,购进两把A型测温枪和三把B型测温枪共需2100元.(1)、一把A型测温枪和一把B型测温枪的售价分别是多少元?(2)、根据学校实际情况,学校共需测温枪30把,县教科体局给学校的预算为1万元,为了不超出预算,学校最多可购进B型测温枪多少?20. 在平面直角坐标系中,A(a,0),B(b,0),C(−1,2),且| |+ =0, (1)、求a、b的值;(2)、在y轴上是否存在一点M,使△COM的面积为△ABC面积的 ,若存在,求出点M的坐标;若不存在,请说明理由.21.(1)、已知两个连续正整数a、b, ,求ab的值.(2)、已知a是 的整数部分,b是 的小数部分,求 的值.(3)、已知 的小数部分为m, 的小数部分为n,求m+n的值.22. 如图1,在平面直角坐标系中,点O为坐标原点,点A(3a,2a)在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,S△AOB=12,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点B出发以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,连接AM,AN,MN.
(1)、求a、b的值;(2)、在y轴上是否存在一点M,使△COM的面积为△ABC面积的 ,若存在,求出点M的坐标;若不存在,请说明理由.21.(1)、已知两个连续正整数a、b, ,求ab的值.(2)、已知a是 的整数部分,b是 的小数部分,求 的值.(3)、已知 的小数部分为m, 的小数部分为n,求m+n的值.22. 如图1,在平面直角坐标系中,点O为坐标原点,点A(3a,2a)在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,S△AOB=12,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点B出发以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,连接AM,AN,MN. (1)、求a的值;(2)、当0<t<2时,
(1)、求a的值;(2)、当0<t<2时,①请探究∠ANM,∠OMN,∠BAN之间的数量关系,并说明理由;
②试判断四边形AMON的面积是否变化?若不变化,请求出其值;若变化,请说明理由。
(3)、当OM=ON时,请求出t的值。