云南省大理州巍山县2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、填空题
-
1. 实数 的平方根是.2. 如图,直线a、b被第三条直线c所截,如果a b,∠1=50°,那么∠2= .
 3. 已知二元一次方程 4x+3y=9,若用含 x 的代数式表示 y,则有 y=.4. 在实数 , -2 , , ,3.14 , , ,这7个数中,其中无理数是5. 已知 是方程 bx﹣2y=10 的一个解,则 b=.6. 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.观察图中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第n个正方形(实线)四条边上的整点个数共有个.
3. 已知二元一次方程 4x+3y=9,若用含 x 的代数式表示 y,则有 y=.4. 在实数 , -2 , , ,3.14 , , ,这7个数中,其中无理数是5. 已知 是方程 bx﹣2y=10 的一个解,则 b=.6. 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.观察图中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第n个正方形(实线)四条边上的整点个数共有个.
二、单选题
-
7. 为了了解全校七年级300名学生的视力情况,李老师从中抽查了50名学生的视力情况.针对这个问题,下面说法正确的是( ).A、300名学生是总体 B、每名学生是个体 C、50名学生是所抽取的一个样本 D、这个样本容量是508. 如图,不能判定AB∥CD的条件是( )
 A、∠B+∠BCD=180° B、∠1=∠2 C、∠3=∠4 D、∠B=∠59. 一个正方形的面积是15,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间10.
A、∠B+∠BCD=180° B、∠1=∠2 C、∠3=∠4 D、∠B=∠59. 一个正方形的面积是15,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间10.如图天平右盘中的每个砝码的质量都是1g,则物体A的质量m(g)的取值范围在数轴上可表示为( )
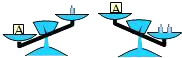 A、
A、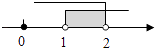 B、
B、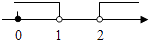 C、
C、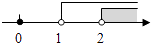 D、
D、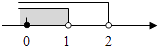 11. 方程组 的解为 ,则被遮盖的前后两个数分别为( )A、1、2 B、1、5 C、5、1 D、2、412. 如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
11. 方程组 的解为 ,则被遮盖的前后两个数分别为( )A、1、2 B、1、5 C、5、1 D、2、412. 如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( ) A、(1,0) B、(-1,0) C、(-1,1) D、(1,-1)13. 在同一平面内,a,b,c是直线,下列说法正确的是( )A、若a∥b,b∥c,则a∥c B、若a⊥b,b⊥c,则a⊥c C、若a∥b,b⊥c,则a∥c D、若a∥b,b∥c,则a⊥c14. 扬州某中学七年级一班40名同学第二次为四川灾区捐款,共捐款2000元,捐款情况如下表:
A、(1,0) B、(-1,0) C、(-1,1) D、(1,-1)13. 在同一平面内,a,b,c是直线,下列说法正确的是( )A、若a∥b,b∥c,则a∥c B、若a⊥b,b⊥c,则a⊥c C、若a∥b,b⊥c,则a∥c D、若a∥b,b∥c,则a⊥c14. 扬州某中学七年级一班40名同学第二次为四川灾区捐款,共捐款2000元,捐款情况如下表:捐款(元)
20
40
50
100
人数
10
8
表格中捐款40元和50元的人数不小心被墨水污染已看不清楚、若设捐款40元的有x名同学,捐款50元的有y名同学,根据题意,可得方程组( )
A、 B、 C、 D、三、解答题
-
15.(1)、计算(2)、用加减法解方程组16. 解不等式组,并把解集在数轴上表示出来 .17. 如图所示,直线a、b被c、d所截,且a⊥c,b⊥c,∠1=70°,求∠3的度数.
 18. 列方程组解应用题:甲、乙两人相距6千米,两人同时出发相向而行,1小时相遇;同时出发同向而行,甲3小时可追上乙.(1)、根据题意画出示意图,分为相向而行、同向而行两种;(2)、求两人的平均速度各是多少?19. 当k取何值时,等式 的b是负数.20. 如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
18. 列方程组解应用题:甲、乙两人相距6千米,两人同时出发相向而行,1小时相遇;同时出发同向而行,甲3小时可追上乙.(1)、根据题意画出示意图,分为相向而行、同向而行两种;(2)、求两人的平均速度各是多少?19. 当k取何值时,等式 的b是负数.20. 如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).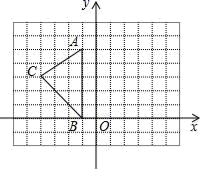 (1)、△ABC的面积是.(2)、在图中画出△ABC向下平移2个单位,向右平移5个单位后的△A1B1C1.(3)、写出点A1 , B1 , C1的坐标.21. 体育委员统计了全班同学60秒跳绳的次数,列出了频数分布表和频数分布直方图.如图:
(1)、△ABC的面积是.(2)、在图中画出△ABC向下平移2个单位,向右平移5个单位后的△A1B1C1.(3)、写出点A1 , B1 , C1的坐标.21. 体育委员统计了全班同学60秒跳绳的次数,列出了频数分布表和频数分布直方图.如图:60≤x<80
80≤x<100
100≤x<120
120≤x<140
140≤x<160
160≤x<180
180≤x<200
2
a
18
13
8
4
1
 (1)、频数分布表中a=;补足频数分布直方图.(2)、上表中组距是 , 组数是组,全班共有人.(3)、跳绳次数在100≤x<140范围的学生有人,占全班同学的%.(4)、从图中,我们可以看出怎样的信息?(合理即可)22. 推理填空.
(1)、频数分布表中a=;补足频数分布直方图.(2)、上表中组距是 , 组数是组,全班共有人.(3)、跳绳次数在100≤x<140范围的学生有人,占全班同学的%.(4)、从图中,我们可以看出怎样的信息?(合理即可)22. 推理填空.如图,EF∥AD,∠1=∠2,∠BAC=70°.
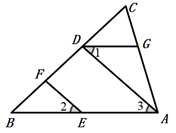
将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= ▲ ( ▲ )
又因为∠1=∠2
所以∠1=∠3( ▲ )
所以AB∥ ▲ ( ▲ )
所以∠BAC+ ▲ =180°( ▲ )
因为∠BAC=70°
所以∠AGD= ▲
23. 为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.(1)、求购买A型和B型公交车每辆各需多少万元?(2)、预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?(3)、在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?